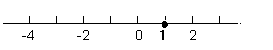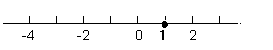Linear Equations in One Variable
This section deals with linear equaitons where you only have one variable. That we will deal with linear equations means that the variable will always be to the first power and only one unknown (the variable) will be found in the equations.
Here are three sample equations :
- 3x = 6 - x is the variable, 3 is the coefficient of x and 6 is a constant.
- 2r = 25 - r is the variable, 2 is the coefficient of the r on the left side of the equation and 25 is a constant.
- 3q + 7 = q - 4 - q is the variable, 3 is the coefficient of the q term to the left of the equals sign, 1 is the coefficient of the q term on the right side of the equaiton and 7 and -4 are constants.
Solving Linear Equations in One Variable - Case 1
Steps to solving ax = b, a and b constants, x is the variable
- The a is multiplied times the x. We want the equation to read x = where the x coefficient is a 1
- So, divide both sides of the equation by a: ax/a = b/a
- Simplify, giving x = b/a
- An example
- Given: 3x = 12 and we want to solve for the value of x that makes this true.
- Divide both sides by 3 giving: (3x)/3 = 12/3
- x = 4, this is the solution.
- To check it we can substitute 4 for x in the original equation
- 3(4) = 12, since 3(4) = 12 we have 12 = 12 so this is the correct solution.
- If you were asked to graph this result you would draw a horizontal number line and put a mark at 4 (usually a filled in circle)

Now it is your turn. The first equation is -2x = 14. If you click the "Click to show problem" button it will appear When you are done hit the button that says "Click to Show Answer" and it will display the answer in a step-by-step manner. After you finish the first problem and look at the answer you can click on the show problem button again and a second problem will appear. It you want to try both problems again hit the "Reset" button.
Solving Linear Equations in One Variable - Case 2
Steps to solve ax + b = cx + d where a and c are coefficients of x and b and d are constants
- We want to get all of the x terms on one side of the equation and all of the other terms on the other side of the equation
- So, we will subtract cx from both sides of the equation and we will also subtract b from both sides of the equation
- ax +b -cx - b = cx + d -cx - b
- Reordering terms gives: ax - cx + b - b = cx -cx + d -b
- Simplifying: ax - cx = d - b
- Factoring the x: x(a - c) = (d - b)
- Divide both sides by (a - c): [x (a - c)]/(a - c) = (d - b)/(a - c)
- Cancel the (a - c) terms: x = (d - b)/(a - c)
- An example
- Given: 5x - 7 = 8x - 10
- Subtract 8x from both sides and add +7 to both sides
- 5x - 7 - 8x + 7 = 8x - 10 - 8x + 7
- Reorder terms: 5x - 8x - 7 + 7 = 8x - 8x - 10 + 7
- Simplify: -3x = -3
- Divide both sides by -3: -3x/(-3) = -3/(-3)
- Simplify: x = 1, this is the solution
- To check replace x in the original equation with 1
- 5(1) - 7 = 8(1) - 10
- Simplify 5 - 7 = 8 - 10
- Simplify: -2 = -2 which is true so our answer checks, x = 1 satisfies the equation
- I we were asked to graph our answer we would put a dot at +1