- The following factors will be used to analyze the behavior of rational functions;
- The zero(es), which we will obtain by finding the values of x that make the numberator zero (N(x) = 0). The zeroes represent the points where the rational function crosses or touches the x axis.
- The vertical asymptote(s), which we will determining the values of x that make the denominator equal to zero (D(x)=0). Vertical asymptotes can be thought of as vertical lines that the function approaches but does not touch. A rational function does not go through a vertical asymptote (doesn't take on that value of x).
- The horizon asymptote, which we will define by taking the highest power of x in the numberator, along with its coefficient and dividing it by the highest power of x in the denominator along with its coefficient. The rules for the calculations are given below.
- The y axis intercept, which is determined by setting x equal to zero and finding the corresponding value of y (if it exists).
- The height above or below the x axis of the function for various values of x. This will be used to determine if the function is above or below the x axis or some horizontal asymptote.
Zeroes - To determine the zeroes of the rational function take the numberator, set it equal to zero and solve for the values of x.
Examples
- N(x) = 2x - 3, set N(x) = 0, 2x - 3 = 0, x = 3/2 so the function crosses the x axis at x = 3/2
- N(x) = x2 - x, set N(x) = 0, x2 - x = 0, factoring gives: x(x-2) = 0, so, x = 0 and x = 2 are zeroes of the function.
- N(x) = 16, set N(x) = 0, 16 = 0, this is never true so there are no zeroes for this function (it does not cross or touch the x axis)
- N(x) = 2x, set N(x) = 0, 2x = 0, x = 0, this function crosses the x axis at the origin.
Asymptotes - We have defined two polynomials that make up a rational function. The numerator polynomial is labeled N(x) and the denominator polynomial will be D(x).
- Vertical Asymptotes: To find the vertical asymptotes set D(x) = 0 and solve for the values of x. Examples:
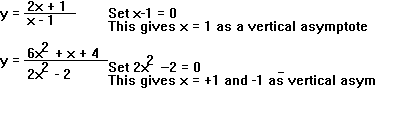
- Horizontal Asymptotes: We will consider three cases
- Degree of N(x) lower than degree of D(x). In this case the value of the fraction will approach zero as x becomes larger and larger in absolute value, and the graph will be asymptotic to the x-axis. Example:

- Degree of N(x) same as that of D(x). In this case, as x becomes larger and larger in absolute value, the value of the fraction approaches a number which is equal to the ratio of the coefficients of the terms in the numberator and denominator that have the highest powers of x. Example:
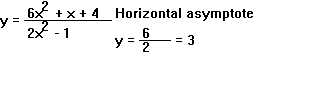
- Degree of N(x) higher than that of D(x). There is a special case when the Degree of N(x) is one higher than the degree of D(x). In that case you will have a slant asymptote. To find the asymptote divide N(x) by D(x) to get the equation of the asymptote. Speaking more generally if the highest power of x in the numerator is greater thant he highest power of x in the denominator the rational function will not have a horizontal asymptote. Example:
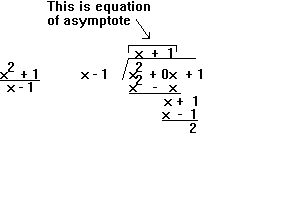
Y axis intercept - To determine the y axis intercept set x equal to zero and solve for the value of y.
Examples
- r(x) = (2x - 3)/ (x2-1), set x = 0 and r(0) = (0 - 3)/(0 - 1) = 3, so the function intercepts the y axis at the point (0,3)
- r(x) = 14/[(x - 7)(x-2)], set x =0 and r(0) = 14/[(-7)(-2)] = 1, so the function intercepts the y axis at the point (0,1)
- r(x)= 3x - 5/[x (x-1)], set x = 0 and r(0) = -5/[0 (-1)] = -5/0 = undefined, this function does not intercept the y axis.