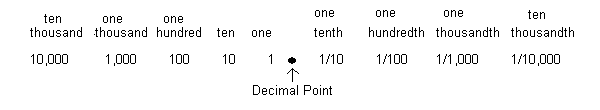Fractions and Decimals

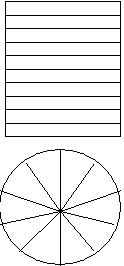Fractions are used to represent a portion of a whole. For example figure on the right shows a box divided into ten parts. The area of each rectangle represents 1/10 of the area of the box. If we wanted half of the box we would take 5 rectangles. They come to 5/10 of the box or 1/2 of the box (5/10 - 1/2). Similarly the circle shown on the right has been divided into ten parts. The portion of the area of the circle in each division can be written as a fraction as 1/10. Each piece represents 1/10 of the area of the circle. Another way to express the same kind of idea is to use decimals. If we wanted 8 of the pieces we could express this as a fraction as 8/10 we want 8 of the 10 pieces of the box.

The ideas represented above can also be written in terms of decimals. If we divide 5 by 10 the answer comes out 0.50 which is five-tenths. Similarly for the circle if we divide 8 by 10 we get 0.80 or eight-tenths. The decimal is based on our numbering system which uses a factor of 10. If you look at decimals you will see that each position to the right or the left of the decimal point represents division or multiplication by 10. The figure show below illustrates this for the numbers that go from one-tenthousandth to ten thousand.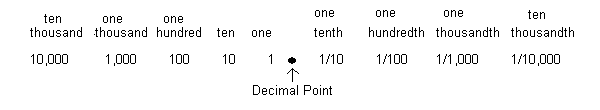

This tells you that position relative to the decimal point determines the value of number. In the number 269 the 2 tells us that we have two hundred, the 6 is in the tens column so we have 6x10 or 60 and the 9 is in the ones column so it stands for 1x9 or 9. Together they tell us we have two hundred and sixty nine. Similarly the number 0.236 tells us that we have two tenths, three hundredths and six thousandths which we would say as two hundred thirty-six thousandths. If we have a whole number with a decimal point and following numbers we put the two parts together. Thus 15.82 can be thought of as 1 in the tens column, 5 in the ones column, the decimal point, 8 in the tenths column and 2 in the hundredths column. We actually say the number as 15 and 82 hundredths.

The key here is to first determine which column a digit is in relative to the decimal point. This allows us to interpret the meaning of the number. Knowing this it should be easy to go from decimals to fractions or fractions to decimals. Here are some examples:

decimal to fraction
• 0.23 = 23/100 written as twenty three hundredths
• 0.0801 = 801/10,000 written as eight hundred one ten-thousandths (four places to the right of the decimal point)
• 0.0006 = 6/10,000 written as six ten-thousandths
• 3.28 = 3 + 28/100 written as three and twenty-eight one hundredths

fraction to decimal
• 0.67 = 67/100 written as sixty-seven one hundredths
• 0.034 = 34/1,000 written as thrity-four thousandths (the 4 is three places from the decimal point which is the thousandths place)
• 2.67 = 2 and 67/100 or 267/100 (the 2 becomes 200/100) written as two and sixty-seven hundredths.

When dealing with decimals the questions arises as to how to round the decimal to a given number of places. The rule is fairly simple:

Rules for rounding
1. Find the place where the rounding is being done (for example hundredths, thousandths, etc...)
2. Draw a vertical line to the right of that place (between that digit and the next digit)
3. Look at the digit to the right of your vertical line
4. If that digit is 5 or more round your number up 1
5. If that digit is less than 5 drop the digit, do not change your number

An example is in order - Round 267.3486315 to the nearest hundredth
1. 267.3486315 - I have put the 8 in bold to show that we are rounding to that place
2. 267.348|6315 - Added the vertical line
3. There is a 6 to the right of our vertical line
4. A 6 is more than 5 so we will round up by 1 (our rule is 5 or more than 5)
5. 267.349 - We rounded the 8 up 1 to 9

Here is a tool that will give you some rounding practice. The tool will generate random numbers. Your job will be to round them to the nearest tenth, hundredth and thousandth.