How you might actually use the trigonometry you have learned
Students have always pondered the question, "What good is all of this math that I am learning?" This is a legitimate question. Undoubtably you will learn a lot of math that you will never use, even if you live to be quite old. But some of the math you learn is actually useful or at least interesting. Hopefully the example shown above and discussed below will be interesting even though most of you will never design an engine.
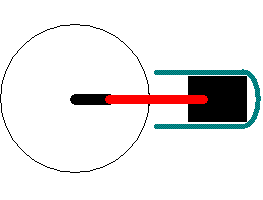
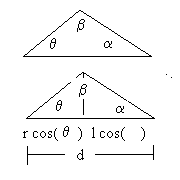 The animation provides a view of a very simple single cylinder engine such as you might find on a lawnmower or a chainsaw. The geometry of the situation in one position is shown on the right. r is the length of a small rod that rotates counterclockwise. For this example I have set r = 2 inches. l is the length of the longer shaft, hooked to the small shaft and the piston and d is the distance between the base of the small shaft and the piston.. For this example I have set l = 5 inches. As the small shaft rotates it pulls and pushes the long rod which in turn pulls and pushes the piston in the cylinder. The problem is more complicated than the example but it should illustrate the point. Angles are defined as α, β, and θ. The only data input that is needed is the time for one revolution in seconds. I have set the period of rotation at 1 revolution per second. This is the period (P) of the function. As you already know P = 2* Π/ B where B is the coeffiecient in the trigonometric function argument (e.g. cos( Bx) ). The default period is one second so for this case 1 = P = 2* π/ B or, solving for B, B = 2* π/P = 2* π/1 = 2* π (in this case). The starting position for the model has both rods in the horizontal plane so the cosine function will be used.
The animation provides a view of a very simple single cylinder engine such as you might find on a lawnmower or a chainsaw. The geometry of the situation in one position is shown on the right. r is the length of a small rod that rotates counterclockwise. For this example I have set r = 2 inches. l is the length of the longer shaft, hooked to the small shaft and the piston and d is the distance between the base of the small shaft and the piston.. For this example I have set l = 5 inches. As the small shaft rotates it pulls and pushes the long rod which in turn pulls and pushes the piston in the cylinder. The problem is more complicated than the example but it should illustrate the point. Angles are defined as α, β, and θ. The only data input that is needed is the time for one revolution in seconds. I have set the period of rotation at 1 revolution per second. This is the period (P) of the function. As you already know P = 2* Π/ B where B is the coeffiecient in the trigonometric function argument (e.g. cos( Bx) ). The default period is one second so for this case 1 = P = 2* π/ B or, solving for B, B = 2* π/P = 2* π/1 = 2* π (in this case). The starting position for the model has both rods in the horizontal plane so the cosine function will be used.
- The horizontal component of r will be r*cos( θ ) = r*cos( 2* π* t) It will vary with time.
- The horizontal component of l will be l*cos( α ) Note that α will also vary with time. We'll cover that in a second
- The distance d will be d = r*cos( θ ) + l*cos α (horizontal component of r plus horizontal component of l)
- For π less than 180o we can use the law of sines to find α
d = black bar horizontal component + or - red bar horizontal component
- sin( θ )/l =sin( θ )/ r
-
- Solveing for sin(θ ) we get sin(θ ) = (r/l) * sin( θ )
- and θ = sin-1[(r/l)* sin( θ )]
- This is easy to see up to 90o
- What happens when π is greater than 90o?
- For π between 90o and 270o the cosine is negative
- In this case the red bar component is negative and is effectively reduces the length d
-
- The table stops at 330o since this is a periodic function and will repeat.
Thinking beyond this simple model you might think of a model for each cylinder with a phase shift from one cylinder to the next. You would also want to determine the times when the spark plug should spark, fuel should be injected into the cylinder, the exhaust value should open and a number of other factors. Some of this can be done with trignometry, some of the model enhancements would require knowledge of physics and chemistry as well as some of the practical aspects of engineering.
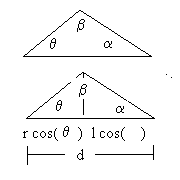 The animation provides a view of a very simple single cylinder engine such as you might find on a lawnmower or a chainsaw. The geometry of the situation in one position is shown on the right. r is the length of a small rod that rotates counterclockwise. For this example I have set r = 2 inches. l is the length of the longer shaft, hooked to the small shaft and the piston and d is the distance between the base of the small shaft and the piston.. For this example I have set l = 5 inches. As the small shaft rotates it pulls and pushes the long rod which in turn pulls and pushes the piston in the cylinder. The problem is more complicated than the example but it should illustrate the point. Angles are defined as α, β, and θ. The only data input that is needed is the time for one revolution in seconds. I have set the period of rotation at 1 revolution per second. This is the period (P) of the function. As you already know P = 2* Π/ B where B is the coeffiecient in the trigonometric function argument (e.g. cos( Bx) ). The default period is one second so for this case 1 = P = 2* π/ B or, solving for B, B = 2* π/P = 2* π/1 = 2* π (in this case). The starting position for the model has both rods in the horizontal plane so the cosine function will be used.
The animation provides a view of a very simple single cylinder engine such as you might find on a lawnmower or a chainsaw. The geometry of the situation in one position is shown on the right. r is the length of a small rod that rotates counterclockwise. For this example I have set r = 2 inches. l is the length of the longer shaft, hooked to the small shaft and the piston and d is the distance between the base of the small shaft and the piston.. For this example I have set l = 5 inches. As the small shaft rotates it pulls and pushes the long rod which in turn pulls and pushes the piston in the cylinder. The problem is more complicated than the example but it should illustrate the point. Angles are defined as α, β, and θ. The only data input that is needed is the time for one revolution in seconds. I have set the period of rotation at 1 revolution per second. This is the period (P) of the function. As you already know P = 2* Π/ B where B is the coeffiecient in the trigonometric function argument (e.g. cos( Bx) ). The default period is one second so for this case 1 = P = 2* π/ B or, solving for B, B = 2* π/P = 2* π/1 = 2* π (in this case). The starting position for the model has both rods in the horizontal plane so the cosine function will be used.
