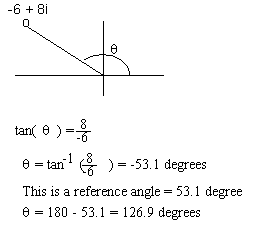Complex Numbers and DeMoivre's Theorem
Complex Numbers- In previous math classes you have probably come upon an equation of the form x2+4 = 0
When you attempted to solve this equation you got x = Square root(-4) and your instructor probably said that is a non-real solution and we will not deal with that is this class. Well, this is the class that will deal with that problem. We will define the square root of -1 to equal i. If we have a quantity such as 3i we will call that an imaginary number (an unfortunate name that comes to us from history). If one of these special numbers has a real part and an imaginary part we will call it a compex number. In cartesian form we will write compex numbers a + bi, where a is the "real" part of the number and "bi" is the imaginary part of the number. Examples of complex numbers are shown below:
- 3 + 2i
- -4 + i
- -2 - 3i
- 5 -2i
- 0 + 3i
- 5 - 0i
Graphs/Plots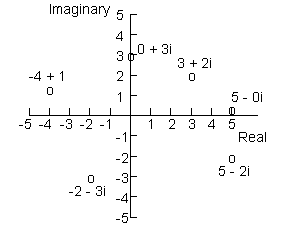 - If we want to graph complex numbers we can use a set of cartesian coordinates (x, y) that has the real part on the horizontal axis and the imaginary part of the number on the vertical axis. The numbers shown above are plotted on the graph to the right. You plot complex numbers in a manner very similar to that used to plot x,y coordinates. The real part goes on the x axis and the imaginary part goes on the y axis. So 3 + 2i means 3 units to the right of the origin and then 2 units up. Now that we can graph complex numbers we will next look at the ways we can manipulate them. Specifically, we will look at addition, subtraction, multiplication and division.
- If we want to graph complex numbers we can use a set of cartesian coordinates (x, y) that has the real part on the horizontal axis and the imaginary part of the number on the vertical axis. The numbers shown above are plotted on the graph to the right. You plot complex numbers in a manner very similar to that used to plot x,y coordinates. The real part goes on the x axis and the imaginary part goes on the y axis. So 3 + 2i means 3 units to the right of the origin and then 2 units up. Now that we can graph complex numbers we will next look at the ways we can manipulate them. Specifically, we will look at addition, subtraction, multiplication and division.
Addition and Subtraction - When adding or subtracting complex numbers you will group real with real and imaginary with imaginary. This is very similar to the concept of grouping "like" terms. Real terms are "like" other real terms and imaginary terms are "like" other imaginary terms. Here are some examples:
- Addition
- (2 + 4i) + (3 + 6i), grouping like terms, (2 + 3) + (4i + 6i) = 5 + 10i
- (3 - 6i) + (-8 + 2i), grouping like terms, [3 + (-8)] + [-6i + 2i] = -5 - 4i
- Subtraction
- (6 + 7i) - (2 + 4i) = 6 + 7i) -2 - 4i, grouping like terms = (6 - 2) + (7i - 4i) = 4 + 3i
- (-8 +3i) - (7 - i) = (-8 + 3i) -7 + i, grouping like terms = (-8 -7) + (3i + i) = -15 + 4i
Multiplication - When multiplying complex numbers the FOIL (First, Outer, Inner, Last) technique that you (probably) learned in previous math classes will do the job. So to multiply (6 - 7i) times (2 + 4i) we would proceed as follows:
- (6 - 7i) * (2 + 4i) = 12 + 24i - 14i - 28i2, grouping like terms and remembering that i2 = -1
- (12 + 28) + (24i - 14i) = 40 + 10i
As a second example we will multiply (-3+ 2i)*(-3 - 2i)
- (-3 + 2i)*(-3 - 2i) = 9 + 6i - 6i -4i2 = 9 + 4 = 13 + 0i, the imaginary part of the number if zero.
- A pair of complex numbers like (a + bi) and (a-bi) are called complex conjugates. When they are multiplied the complex part will always be zero. We will use that fact to help us divide complex numbers.
Division - Suppose we want to divide 3 - 6i by 2 + 4i. To do this we will:
- Form the complex conjugate of the denominator, in this case 2 - 4i (change the middle sign and only the middle sign)
- Multiply the basic fraction by 1 but write 1 as (2 - 4i)/(2 - 4i)
- Simplify the result
Now we will use numbers
- [(3 - 5i)/(2 + 4i)] * [(2 - 4i)/(2 - 4i)]
- Multiplying numerator terms gives: 6 - 12i - 10i - 20i2 = 26 - 22i
- Multiplying denominator terms gives: 4 - 8i + 8i -16i2 = 20 + 0i (no imaginary component)
- Final result: 26/20 - 22i/20 = 13/10 - (11/10)i = 1.3 - 1.1i
Forms of Complex Numbers At this point we have looked at the basics of complex numbers. The next step is to look at the various forms of the complex number and then to do some mathematics with the various forms. Your text books (Connally and Durbin) cover three forms of the complex number. These are:
- The cartesian form: a + bi
- The trigonometric form: r [cos(q) + i sin(q)] - where r is the absolute value of the complex number and q is an angle
- The Polar form: reiq - where r is the absolute value of the complex number and q is an angle but must be in radians
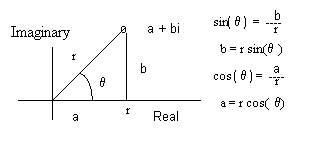 Trigonometric FormWe have already looked at the cartesian form. The next form we will look at is the trigonometric form. To the right you see a plot of the point a + bi. The length along the horizontal axis is a, the length in the vertical plane is b. The angle to the point, measured counterclockwise from the horizontal axis is theta. The trigonometric functions of the angle are shown in the figure the sine is equal to b/r and the cosine to a/r, where r is the absolute value of the complex number. When we solve the two trigonometric equations for a and b we get b = r sin(q) and a = r cos(q). It we next substitute these values into a + bi we get r cos(theta) + i * r sin(theta).
Factoring r gives, r[ cos(q) + i sin(q)] which is the trigonometric form of the complex number. So to convert the a + bi form to trigonometric form you:
Trigonometric FormWe have already looked at the cartesian form. The next form we will look at is the trigonometric form. To the right you see a plot of the point a + bi. The length along the horizontal axis is a, the length in the vertical plane is b. The angle to the point, measured counterclockwise from the horizontal axis is theta. The trigonometric functions of the angle are shown in the figure the sine is equal to b/r and the cosine to a/r, where r is the absolute value of the complex number. When we solve the two trigonometric equations for a and b we get b = r sin(q) and a = r cos(q). It we next substitute these values into a + bi we get r cos(theta) + i * r sin(theta).
Factoring r gives, r[ cos(q) + i sin(q)] which is the trigonometric form of the complex number. So to convert the a + bi form to trigonometric form you:
- Calculate the absolute value of the complex number, r (square root of a2 + b2)
- substitue r cos(q) for a and r sin(q) for b
- factor the r to get r[ cos(q) + i sin(q)]
Polar FormYour text book tells you (I hope!) that Euler developed the formula eiq = cos(q) + i sin(q). If you multiply both sides of this equation by r you get the expression reiq = r[cos(q) + i sin(q)]. This is the Polar form of the a complex number. To convert from either of the other forms we need only find r (the absolute value of the complex number) and q the angle (in radians).
Converting from one Form to Another - Examples
Cartesian to Trigonometric and Polar - Assume we have a complex number of the form 3 + 4i.
- Find the absolute value - square root [32 + 42] = square root[ 9 + 16] = 5, so r = 5
- Find q - the point 3 + 4i is a first quadrant point so the angle we want will be a first quadrant angle. tan(q) = 4/3 and tan-1(4/3) = 0.9273 radians.
- Trigonometric form is: 5 [cos(q) + i sin(q)]
- Polar form is : 5 e0.9273i
Trigonometric to Cartesian and Polar - Assume we have a complex number of the form 8 [cos(2.2166) + i sin(2.2166)]
- The absolute value is given as 8
- The angle q is given as 2.2166 radians. 2.2166 radians places this angle is the second quadrant.
- a = 8 cos(2.2166) = -0.6018 and b = 8 sin(2.2166) = 0.7986, the complex number is cartesian form is -0.6018 + 0.7986 i
- In Polar form the number is 8 e2.2166i
Polar to Cartesian and Trigonometric - Assume we are given a complex number of the form 2.5 e5.9721i
The absolute value is given as 2.5
The angle q is given as 5.9721 radians
a = 2.5 cos(5.9721) = 2.3800, b = 2.5 sin(5.9721) = -0.7652 and the number in cartesian form is 2.3800 - 0.7652 i
r = 2.5 and q = 5.9721 so the Trigonometric form is 2.5 [cos(5.9721) + i sin(5.9721)]
DeMoivre's Theorem - To this point we have covered the basics of complex numbers. The next question we will address is taking a complex number to a power followed by finding the roots of a complex number. Let's start with the question of taking a complex number to a power by first looking at multiplying two complex numbers.
If they are in a + bi format we can FOIL them. For example, given 3 + 2i and 6 - 7i
- (3 + 2i) (6 - 7i) = 18 -21i +12i -14 i2 = 18 + 14 - 9i = 32 + 91
- If we had several numbers to multiply or if we wanted to find (a + bi)6 this could get cumbersome.
If they are in reiq we can multiply the r values and add exponents. For example:
- [2e2.1i][3e0.4i] = 6e2.4i
- If we wanted to find powers of a number this format leads t easy solutions. For example consider [2e2.1i]6
- This would become 26*e6*2.1i = 64e12.6i
- This is much easier than doing a number of FOILs to get the same result
If the numbers are in trigonometric format the result is almost as simple. If we have {2[cos(q) + i sin(q)]}6 we can use DeMoivre's Theorem to write
- = 26[cos(6q) + i sin(6q)].
- Durbin devlopes this idea. It says if you have a complex number in trigonometric form and take it to the nth power the result is the absolute value to the nth power (rn times cos(nq) + i sin(nq). (Durbin page 358 near the top).
- [3 (cos(q) + i sin(q)]4 = 34 * [cos(4q) + i sin(4q)]
An example - Suppose we have the complex number -6 + 8i and we want to take it to the third power. First we will convert it to trigonometric form and then we will use DeMoivre's Theorem to take the trigonomeric form to the third power.
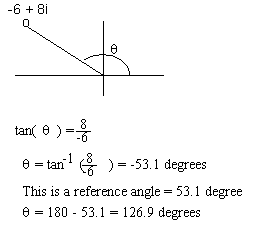
- We need to find r, r = Square root [ 62 + 82] = Square root ( 36 + 64) = Square root(100) = 10
- Now we need to find a value for q).
- We know that q) is a second quadrant angle. If in doubt look at the figure to the right where we have plotted the complex number -6 + 8i. Clearly we are in the second quadrant.
- The calculation of the reference angle yields a value of 53.1o and an angle of 126.9o.
- So, (-6 + 8i)3 = [10 (cos126.9o + i sin12..9o)]3
- = 10o [cos(3 * 126.9o) + i sin(3 * 126.9o)]
- = 1000(cos 380.7o + i sin 380.7o), since 380.7 has the same terminal side as 20.7o
- we can write 1000(cos 20.7o + i sin 20.7o)
- If we want a + bi we get 935.444 + i 353.475
- In Polar form we convert 20.7o to 0.3613 r to get 1000e0.3613i
Find the roots of a Complex Number To end this section let's look at the problem of finding the roots of a complex number. When we took the number to a power we converted to trigonometric form and then used the relationship:
(a + bi)n = [r (cosq + i sinq]n
Which is equal to rn [ cos(n * q) + i sin(n * q)]
If we have the above result and go want to go backwards it seems obvious that we will have to take the nth root of rn and divide the arguments of cos(n*q) and sin(n*q) by n. This is almost correct. There is one adjustment that we must make. In the example worked just before this our final answer was 380.8 degrees but we wrote it as 380.8o - 360sup>o = 20.8sup>o. It made no difference to our answer and simplified the equation. But, it says that when we have a solution and are going for a root we don't really know the actual solution. So we will write (q + k360o) and divide that by n. If we are working in radians we will add k2p instead of 360o. Then we will let k vary from 0 to 1 to 2 and calculate results only stopping when our angle exceeds the usual limit of 360o. In actual practice if it is a third root there will be three answers, if it is an nth root there will be n answers and we will quit when k = n - 1.
An Example - Let's find the cube roots of -i.
- r = square root [ 02 + (-1)2] = 1
- q = 270o
- So we have in trigonometric form [ 1 * (cos 270o + i sin o]1/3]
- The cube root of 1 is 1 so we have 1 * {cos[(270o + k 360o)/3] + i sin[(270o + k 360o)/3].
- = cos(90o + k 120o) + i sin(90o + k 120o)
- k = 0 gives: cos(90o + i sin(90o)
- k = 1 gives: cos(210o + i sin(210o)
- k = 2 gives: cos(300o + i sin(300o)
- k = 3 gives us a value of 90o + 360o) which exceeds our limit and is therefore too big and we stop.
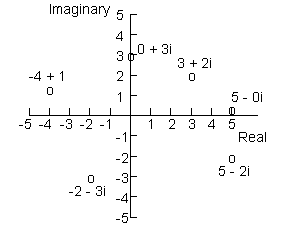 - If we want to graph complex numbers we can use a set of cartesian coordinates (x, y) that has the real part on the horizontal axis and the imaginary part of the number on the vertical axis. The numbers shown above are plotted on the graph to the right. You plot complex numbers in a manner very similar to that used to plot x,y coordinates. The real part goes on the x axis and the imaginary part goes on the y axis. So 3 + 2i means 3 units to the right of the origin and then 2 units up. Now that we can graph complex numbers we will next look at the ways we can manipulate them. Specifically, we will look at addition, subtraction, multiplication and division.
- If we want to graph complex numbers we can use a set of cartesian coordinates (x, y) that has the real part on the horizontal axis and the imaginary part of the number on the vertical axis. The numbers shown above are plotted on the graph to the right. You plot complex numbers in a manner very similar to that used to plot x,y coordinates. The real part goes on the x axis and the imaginary part goes on the y axis. So 3 + 2i means 3 units to the right of the origin and then 2 units up. Now that we can graph complex numbers we will next look at the ways we can manipulate them. Specifically, we will look at addition, subtraction, multiplication and division.
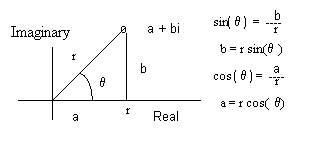 Trigonometric FormWe have already looked at the cartesian form. The next form we will look at is the trigonometric form. To the right you see a plot of the point a + bi. The length along the horizontal axis is a, the length in the vertical plane is b. The angle to the point, measured counterclockwise from the horizontal axis is theta. The trigonometric functions of the angle are shown in the figure the sine is equal to b/r and the cosine to a/r, where r is the absolute value of the complex number. When we solve the two trigonometric equations for a and b we get b = r sin(q) and a = r cos(q). It we next substitute these values into a + bi we get r cos(theta) + i * r sin(theta).
Factoring r gives, r[ cos(q) + i sin(q)] which is the trigonometric form of the complex number. So to convert the a + bi form to trigonometric form you:
Trigonometric FormWe have already looked at the cartesian form. The next form we will look at is the trigonometric form. To the right you see a plot of the point a + bi. The length along the horizontal axis is a, the length in the vertical plane is b. The angle to the point, measured counterclockwise from the horizontal axis is theta. The trigonometric functions of the angle are shown in the figure the sine is equal to b/r and the cosine to a/r, where r is the absolute value of the complex number. When we solve the two trigonometric equations for a and b we get b = r sin(q) and a = r cos(q). It we next substitute these values into a + bi we get r cos(theta) + i * r sin(theta).
Factoring r gives, r[ cos(q) + i sin(q)] which is the trigonometric form of the complex number. So to convert the a + bi form to trigonometric form you: