Inverses, Reference Angles and the Solution of Trigonometric Equations
Ultimately we would like to be able to solve trigonometric equations. To get to that point we are now going to take a couple of preliminary steps. Step one will be to define an inverse function for the sine and cosine. The next step will be the definition of what is called a "reference angle". The two will then be combined into a technique for solving trigonometric equations. First the definition of the inverse function.
Inverse Functions
If we graph a sine or a cosine function and then apply the vertical line test either function passes the test. But to have an inverse that is also a function the graphs must also pass the horizontal line test and both fail this test. As the graph on the right clearly illustrates a horizontal line cuts the graph more than once. This means that there are many possible x values for each value of y. But we want x to be a function of y so there can only by one x for any given y value. To make this happen mathematicians have created the restricted sine, cosine and tangent functions. The domain of the sine, cosine and tangent functions are restricted to a certain portion of the real line. The exact restrictions are as follows:
- For the sine function: -90o <= q <= +90o
- For the tangent function: -90o< q < +90o
- For the cosine function: 0o<= q <= +180o
The input to the inverse sine function is a number between -1 and +1 (including the endpoints) the output of the inverse sine is an angle between -90o and +90o including the endpoints. For the inverse tangent function the inputs are angles between -90o and +90o not including the endpoints and the outputs go from negative infinity to positive infinity. For the inverse cosine the inputs go from 0o to 180o including the endpoints and the outputs vary from -1 to +1.
Lets look at a few examples.
Simple inverses
- sin-1(0.5) = 30o
- cos-1(0.5) = 60o
- tan-1(1.0) = 45o
More complex inverse relationships
- sin[sin-1(0.5)] = sin[30o] = 0.5
- sin[cos-1(0.5)] = sin[60o] = 0.8660
- cos[tan-1(1.0)] = cos[45o] = 0.7071
Still more complex results
- sin-1[sin(150o] = sin-1[0.5] = 30sin-1
- Note that the above example did not give us back the 150o value. 150o is not within the range of the inverse sine function.
Just to give you a little practice, type in a tirgonometric function name: sin, cos or tan (all small letters, just three letters in the name and just these three functions). Now enter a decimal value for the trig function and hit the compute button. Compare your guess to the correct answer. Hopefully yours will be close, if not try to figure out why you are off.
Now let's take things a step further and develop the concept of reference angles. After we have both inverses and reference angles we will look at solving trigonometric equations.
Reference Angles
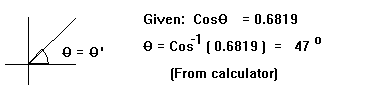 A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
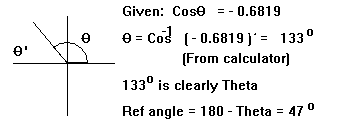 In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
 None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
 In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
-------Signs of the Trigonometric Functions------
| Quadrant | Sine | Cosine | Tangent |
|---|
| 1 | + | + | + |
| 2 | + | - | - |
| 3 | - | - | + |
| 4 | - | + | - |
Why are we so interested in reference angles? The main reason is that the absolute value of an angles trigonometric function will be exactly the same as the absolute values of the same trigonometric function for the reference angle. To get the proper sign we merely need to know the quadrant. This means that by using reference angles and inverses we can find the value of any angle. Let's next look at some simple trigonometric equations and solve them using these two tools.
Solving Trigonometric Equations - At this point you are ready to solve some trigonometric equations. This is probably best attacked by working some examples. Listed below are four examples that we will work. In each case we will limit the domain of the solution set to [0o, 360o). If we did not limit the domain you would have to add k*360o or k*2p to each solution to allow for the repeating nature of the function.
- sin(q) = 1/2
- cos2(q) - cos(q) = 0
- sin2(q) - 2sin(q) - 3 = 0
- 7sin(q) +1 = 0
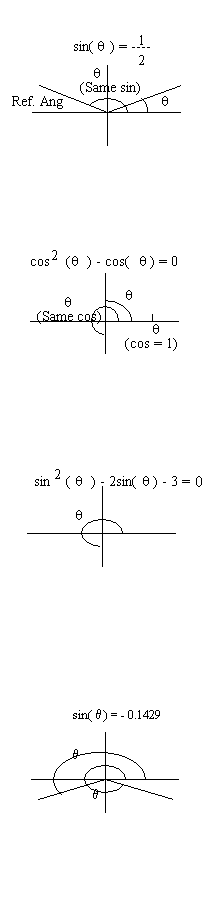 Problem 1 - We are given that sin(q) = 1/2.
Problem 1 - We are given that sin(q) = 1/2.
Soltution Steps
- In which quadrants could sin(q) = 1/2, only in quadrants 1 and 2 is the sin positive.
- What angle has a sine of 1/2? Sin-1(1/2) = 30o. So 30o is one solution and the reference angle for a second quadrant solution. The second quadrant angle will be 180o - 30o = 150o.
- So, the two solutions to our equation are 30o and 150o
- Note that unlike algebraic equations a linear trigonometric equation may have more than one solution.
Problem 2 - We are given that cos2(q) - cos(q) = 0
Solution Steps
- The temptation here is to divide by cos(q), that would be a mistake. How would you know that you were not dividing by zero?
- The correct thing to do is to factor out cos(q) which is a common factor to both terms. This leaves you with cos(q)*(cos(q) - 1) = 0
- Now you can set each factor equal to 0 (just as you did when you solved algebraic equations)
- cos(q) = 0 and q = 90o and 270o.
- cos(q) - 1 = 0, so cos(q) = 1, which has one solution, q = 0o
- This equation has three solutions 0o, 90o, and 270o.
Problem 3 - We are given that sin2(q) - 2sin(q) - 3 = 0
Solution Steps
- First, you must recognize that you will have to factor this equation before solving. If it won't factor your best bet would be to use the quadratic formula (since it is a quadratic equation).
- Factoring gives: (sin(q) - 3)*(sin(q) + 1) = 0
- Now set each factor equal to 0
- sin(q) - 3 = 0 or sin(q) = 3, this has no solutions because the sine of an angle is never greater than 1
- sin(q) + 1 = 0 gives sin(q) - 1, the solution for this is q = 270o
- This equation has only one real solution, even though it is a quadratic equation.
Problem 4 - The given equation is: 7sin(q) +1 = 0
Solution Steps
- First we solve for sin(q)and get sin(q) = -1/7 = -0.1429
- Now we need to determine where this can occur. The sine will be negative in quadrants 3 and 4. So, we have two possible solutions, one in quadrant 3 and one in quadrant 4.
- Our next step is to find the reference angle. sin-1(|-0.1429|} = 8.22o.
- The third quadrant solution will be 180o + 8.22o. = 188.22o
- The fourth quadrant solution will be 360o - 8.22o = 351.78o.
- Our equation has the two solutions shown above.
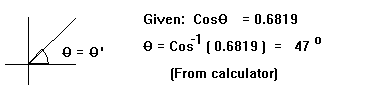 A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
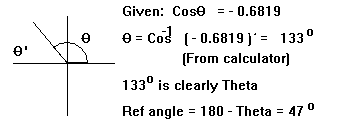 In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
 None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
 In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
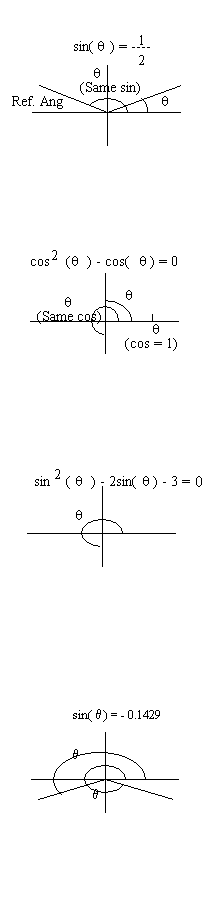 Problem 1 - We are given that sin(q) = 1/2.
Problem 1 - We are given that sin(q) = 1/2.