General Triangles

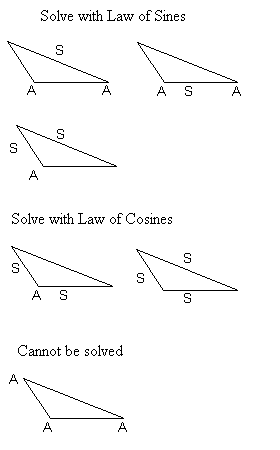
In this section we will look at triangles that do not contain a right angle. We will be interested in "SOLVING" the triangles. Solving a triangle means find the size of all of the angles and sides that make up the triangle. As a start let's consider six possible states of knowledge about the triangles that we will be attempting to solve. We will label angles with the letter A and sides with the letter S. Here are the possible starting conditions, the letters representing what we know.

Solve with Law of Sines
1. AAS - We know two angles and a side. We can find the third angle by adding the two known angles and subtracting from 180^o. Once we have all three angles we can use the Law of Sines to find the unknown sides.
2. ASA - We know two angles and the side that lies between them. We can find the third angle by adding the two known angles and subtracting from 180^o. Once we have all three angles we can use the Law of Sines to find the unknown sides.
3. ASS - We know an angle and two sides. This is frequently called the ambiguous case We can use the Law of Sines to try to find the second angle. We may find no solutions, one solution or two solutions.

Solve with Law of Cosines
1. SAS We know two sides and the angle between them. Using the Law of Cosines we can find the third side and the other angles (may also use the Law of Sines once we have found the second side).
2. SSS We know all three sides but we don't know any of the angles. Use the Law of Cosines to find one or more of the angles. Once we have more information it is possible to use the Law of Sines to complete the solution.

Cannot be solved
1. AAA We know all three angles but we don't know the length of any of the sides. None of our laws will work for this triangle. While we know the shape of the triangle we don't have a reference for size. There are many triangles that could have the same three angles and we don't know which one is represented by our problem. We need some length to be able to solve this proble.

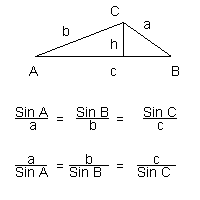The Law of Sines - Consider the triangle shown to the left. If we calculate the sine of A we get Sin(A) = h/b. If we calculate the sine of B we get Sin(B) = h/a. If we solve both of these equations for h we get:

• h = b Sin(A)
• and h = a Sin(B)
• since both equations are h = we can equate them to each other, b Sin(A) = a Sin(B)
• This can be written as Sin(A)/a = Sin(B)/b, This is the Law of Sines
• The full expression of the law is shown to the right.

Let's use the law to solve some problems.

Problem 1 - AAS, Given A = 40^o, B = 30^o and a = 8

• Find angle C = 180^o - (40^o + 30^o) = 110^o
• Find side b, b/Sin(30^o) = 8/Sin(40^o)
• b = 8 Sin(30^o)/Sin(40^o) = 6.22

• Find side c, c/Sin(110^o) = 8/Sin(40^o)
• b = 8 Sin(110^o)/Sin(40^o) = 11.69

To check that our solution is reasonable we arrange the anges in order. The sides should also be in order.
1. 110^o, 11.69
2. 40^o, 8
3. 30^o, 6.22
4. All appears well. The largest side goes with the largest angle, the middle with the middle and the smallest with the smallest

Problem 2 ASS (Ambiguous case - No Solutions) Given that angle A is 80^o, side a is 6 ft and side b is 12 ft.

Find angles B and C and side c
• Sin(B)/12 = sin(80^o)/6
• Sin(B) = (12/6) * sin(80^o)
• Sin(B) = 1.9696
• From the calculator: Sin^-1(1.9696) = ERR"Domain, the sine of an angle is between -1 and +1
• No solutions

Problem 3 ASS (Ambiguous case - One Solution) Given that angle A is 80^o, side a is 13 inches and side b is 12 inches.

Find angles B and C and side c
• Sin(B)/12 = Sin(80^o)/13
• Sin(B) = (12/13) * Sin(80^o)
• Sin(B) = 0.9091
• From the calculator: Sin^-1(0.9091) = 65.4^o
• Answer could also be 180^o - 65.4 = 114.6^o
• But 114.6^o + 80^o = 194.6^o which is more than 180^o so this will not work in a triangle where the sum of the angles must be 180^o.
• So, one solution and angle C = 180^o - (80^o + 65.4^o) = 34.6^o
• Side c is calculated via, c/Sin(34.6^o) = 13/sin(80^o)
• c = 13 * [sin(34.6^o)/sin(80^o)] = 7.5 inches

Problem 4 ASS (Ambiguous case - Two Solutions) Given that angle A is 80^o, side a is 11.86 meters and side b is 12 meters.

Find angles B and C and side c
• Sin(B)/12 = Sin(80^o)/11.86
• Sin(B) = (12/11.86) * Sin(80^o) = 0.9964
• B = Sin^-1(0.9964) = 85.2^o
• B could also be 180^o - 85.2^o = 94.8^o
• 180^o - (98.4^o + 80^o) = 180^o - 178.4^o = 5.2^o which is a fesible solution so this triangle has two possible solutions.

• Angle	Degrees	Angle	Degrees
  A	80.0o	A	80.0o
  B	85.2o	B	94.8o
  C	14.8o	C	5.2o
  Total	180o	Total	180o

• For the left hand solution c/Sin(14.8^o) = 11.86/Sin(80^o)
• c = 11.86 * ]Sin(14.8^o)/Sin(80^o)] =3.08 meters
• and for the right hand solution c/Sin(5.2^o) = 11.86/Sin(80^o)
• c = 11.86 * ]Sin(5.2^o)/Sin(80^o)] = 1.09 meters

Law of Cosines - The Law of Cosines is derrived in the text. Here we will focus on using the law to solve some problems. The figure on the right gives two versions of the Law of Cosides the lefthand side can be found in the text. The righthand side is not in the text but comes from solving the lefthand versions for the cosine of the angle. Both versions are useful. The lefthand version for SAS problems and the righthand version for SSS problems. We will use each version to solve a problem.

Problem 1 SAS - You are at a military observation post. You have line-of-sight to both an friendly patrol and an enemy encampment. You get a laser range to the enemy of 5 km and a range to the friendlies of 6 km. The friendlies want to know how far they are from the enemy. You calculate the distance using the law of cosines.

Calucation of Friendly to Enemy Distance
• d² = 6² + 5² - 2*6*5*cos(27^o)
• d² = 7.5396
• d = 2.75 km

Problem 2 SSS - You are given the triangle shown to the right. You know all three sides but none of the angles. I suggest that in this situation it would be good to find the largest angle first. If that angle is more than 90^o there can only be one solution to the problem (any other second quadrant angle would be too big). So, let's solve for C first.

Solution of SSS problem
• Cos(C) = [6² + 8²- 11²]/[2*6*8] = -0.2188
• C = cos^-1(-0.2188) = 102.6^o
• Cos(A) = [6² + 11² - 8²]/[2*6*11] = 0.7045
• A = cos^-1(0.7045) = 45.2^o
• Cos(B) = [11² + 8² - 6²]/[2*11*8] = 0.8466
• B = cos^-1(0.8466) = 32.2^o
• Just to check: 102.6 + 45.2 + 32.2 = 180^o as it should