The Sine and Cosine Functions
The last section introduced the idea of periodic funcitions. This section will carry that idea forward and look at two specific periodic functions the sine and the cosine. The figures shown below give you a view of the graph of a sine function (on the left) and the graph of a cosine functin (right).
Graph of a Sine Wave | Graph of a Cosine Wave |
|---|
 Where did the graphs come from? To see that lets go back to our triangles inside a circle. As you may remember (hopefully) we said that you could generate an angle by starting with a line along the positive x axis and rotating it counterclockwise for a positive angle and clockwise for a negative angle. The side of the angle along the positive x axis we called the initial side and the line we have when we stopped rotating we called the terminal side of the angle. The angle itself is between those two lines. If we drop a perpendicular line from the point where the terminal side of the angle touches the circumference of our circle we create a right triangle (figure on right). One side of the triangle is x units long and the other side is y units high. The hypotenuse is equal to the radius of the circle. For the situation shown we can calculate the sine of angle A by using our definition sin(A) = opposite/hypotenuse = y/r. Similarly cos(A) = x/r. As we go around the circle we can calculate values of the sine and cosine functions. No matter where we are in the circle r will be positive but x and y will take on different signs as we go around the circle. The table below gives the signs of x and y in each quadrant and the resulting sign of the sine and cosine functions.
Where did the graphs come from? To see that lets go back to our triangles inside a circle. As you may remember (hopefully) we said that you could generate an angle by starting with a line along the positive x axis and rotating it counterclockwise for a positive angle and clockwise for a negative angle. The side of the angle along the positive x axis we called the initial side and the line we have when we stopped rotating we called the terminal side of the angle. The angle itself is between those two lines. If we drop a perpendicular line from the point where the terminal side of the angle touches the circumference of our circle we create a right triangle (figure on right). One side of the triangle is x units long and the other side is y units high. The hypotenuse is equal to the radius of the circle. For the situation shown we can calculate the sine of angle A by using our definition sin(A) = opposite/hypotenuse = y/r. Similarly cos(A) = x/r. As we go around the circle we can calculate values of the sine and cosine functions. No matter where we are in the circle r will be positive but x and y will take on different signs as we go around the circle. The table below gives the signs of x and y in each quadrant and the resulting sign of the sine and cosine functions.
| Quadrant | x | y | sin(A) | cos(A) |
|---|
| I | + | + | y/r = +/+ = + | x/r = +/+ = + |
| II | - | + | y/r = +/+ = + | x/r = -/+ = - |
| III | - | - | y/r = -/+ = - | x/r = -/+ = - |
| IV | + | - | y/r = -/+ = - | x/r = +/+ = + |
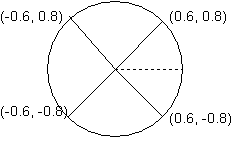 A special case occurs when the radius of the circle is equal to 1. Most textbooks refer to this as the unit circle (meaning the radius is one unit long). In this special case sin(A) = y/r = y/1 = y and cos(A) = x/r = x/1 = x. This means that for the unit circle the x and y coordinates of point P are the cosine and sine of the angle A. This has several uses. First if we know one coordinate we can find the other by using the Pythagorean Theorem and once we have both coordinates we know the sine and cosine of the angle. Secondly if we are given the x and y coordinates of a point on the circumference of the unit circle we automatically know the cosine and sine of the angle (x and y respectively). Let's look at an example in each of the four quadrants (as we go around the circle).
A special case occurs when the radius of the circle is equal to 1. Most textbooks refer to this as the unit circle (meaning the radius is one unit long). In this special case sin(A) = y/r = y/1 = y and cos(A) = x/r = x/1 = x. This means that for the unit circle the x and y coordinates of point P are the cosine and sine of the angle A. This has several uses. First if we know one coordinate we can find the other by using the Pythagorean Theorem and once we have both coordinates we know the sine and cosine of the angle. Secondly if we are given the x and y coordinates of a point on the circumference of the unit circle we automatically know the cosine and sine of the angle (x and y respectively). Let's look at an example in each of the four quadrants (as we go around the circle).
Unit Circle, sine and cosine from (x, y) coordinates of a point.
- In the first quadrant a point on the unit circle has (x, y) coordinates of (0.6, 0.8). This means cos(angle) = 0.6 and sin(angle) = 0.8
- In the second quadrant a point on the unit cirlce has coordinates of (-0.6, 0.8). This means cos(angle) = -0.6 and sin(angle) = 0.8
- In the third quadrant a point on the unit circle has coordinates of (-0.6, -0.8). Cos(angle) = -0.6 and sin(angle) = 0.8
- In the fourth quadrant a point on the unit circle has coordinates of (0.6, -0.8). Cos(angle) = 0.6 and sin(angle) = -0.8
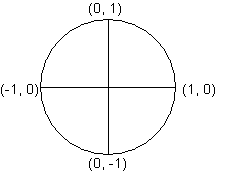 What if our points are along the axes? Let's consider that next. The figure to the right provides information on the coordinates of each point as we go around the unit circle. The calculation of the sine and cosine is shown below:
What if our points are along the axes? Let's consider that next. The figure to the right provides information on the coordinates of each point as we go around the unit circle. The calculation of the sine and cosine is shown below:
Unit Circle (r = 1), sine and cosine of point on an axis.
- Along the positive x axis. Coordinates are (1, 0). Cos(0o) = 1/1 = 1, sin(0o) = 0/1 = 0
- Along the positive y axis. Coordinates are (0, 1). Cos(90o) = 0/1 = 0, sin(90o) = 1/1 = 1
- Along the negative x axis. Coordinates are (-1, 0). Cos(180o) = -1/1 = -1, sin(180o) = 0/1 = 0
- Along the negative y axis. Coordinates are (0, -1). Cos(270o) = 0/1 = 0, sin(270o) = -1/1 = -1
- The next axis would be the positive x axis which we have already calculated.
 Now lets consider what happens when we are on a circle that is not a unit circle. We still drop a perpendicular from each point P to the x axis. Now we have a triangle with sides x, y and r. But in this case r is not equal to 1. Let's let x = 3, y = 4 and r = 5.
Now lets consider what happens when we are on a circle that is not a unit circle. We still drop a perpendicular from each point P to the x axis. Now we have a triangle with sides x, y and r. But in this case r is not equal to 1. Let's let x = 3, y = 4 and r = 5.
- To get sin(A) we have sin(A) = opposite/hypotenuse = y/r = 4/5 = 0.8.
Similarly, cos(A) = adjacent/hypotenuse = 3/5 = 0.6.
What this tells us is that it doesn't matter if we have a unit circle or not, if we know any two of x, y and r we can find the third with the Pythagorean Theorem and then use the values to find the sine and cosine of the angle. Note that we must use the proper sign for x and y if our sin and cos are to come out correctly. X will be + in the first and fourth quadrants, Y will be + in the first and second quadrants and r will always be positive. If we know the angle but want to find x or y we can turn the equations around:
- sin(A) = y/r so, y = r sin(A)
- cos(A) = x/r so, x = r cos(A)
Suppose we know that in a circle of radius 6 sin(C) = 0.2500. Then we can find y as y = 6 sin(c) = 6 (0.2500) = 1.50. If we want to find x we can write x2 = 62 - 1.52 = 36 - 2.25 = 33.75. Taking the square root we get 5.81 (rounded). We could also have used an inverse function sin-1(0.2500) to find the angle, then found the cosine of the angle and finally used x = r cos(C) to find the value of x.
That completes this section. The next section looks at graphs of the sine and cosine functions.
 Where did the graphs come from? To see that lets go back to our triangles inside a circle. As you may remember (hopefully) we said that you could generate an angle by starting with a line along the positive x axis and rotating it counterclockwise for a positive angle and clockwise for a negative angle. The side of the angle along the positive x axis we called the initial side and the line we have when we stopped rotating we called the terminal side of the angle. The angle itself is between those two lines. If we drop a perpendicular line from the point where the terminal side of the angle touches the circumference of our circle we create a right triangle (figure on right). One side of the triangle is x units long and the other side is y units high. The hypotenuse is equal to the radius of the circle. For the situation shown we can calculate the sine of angle A by using our definition sin(A) = opposite/hypotenuse = y/r. Similarly cos(A) = x/r. As we go around the circle we can calculate values of the sine and cosine functions. No matter where we are in the circle r will be positive but x and y will take on different signs as we go around the circle. The table below gives the signs of x and y in each quadrant and the resulting sign of the sine and cosine functions.
Where did the graphs come from? To see that lets go back to our triangles inside a circle. As you may remember (hopefully) we said that you could generate an angle by starting with a line along the positive x axis and rotating it counterclockwise for a positive angle and clockwise for a negative angle. The side of the angle along the positive x axis we called the initial side and the line we have when we stopped rotating we called the terminal side of the angle. The angle itself is between those two lines. If we drop a perpendicular line from the point where the terminal side of the angle touches the circumference of our circle we create a right triangle (figure on right). One side of the triangle is x units long and the other side is y units high. The hypotenuse is equal to the radius of the circle. For the situation shown we can calculate the sine of angle A by using our definition sin(A) = opposite/hypotenuse = y/r. Similarly cos(A) = x/r. As we go around the circle we can calculate values of the sine and cosine functions. No matter where we are in the circle r will be positive but x and y will take on different signs as we go around the circle. The table below gives the signs of x and y in each quadrant and the resulting sign of the sine and cosine functions.
 A special case occurs when the radius of the circle is equal to 1. Most textbooks refer to this as the unit circle (meaning the radius is one unit long). In this special case sin(A) = y/r = y/1 = y and cos(A) = x/r = x/1 = x. This means that for the unit circle the x and y coordinates of point P are the cosine and sine of the angle A. This has several uses. First if we know one coordinate we can find the other by using the Pythagorean Theorem and once we have both coordinates we know the sine and cosine of the angle. Secondly if we are given the x and y coordinates of a point on the circumference of the unit circle we automatically know the cosine and sine of the angle (x and y respectively). Let's look at an example in each of the four quadrants (as we go around the circle).
A special case occurs when the radius of the circle is equal to 1. Most textbooks refer to this as the unit circle (meaning the radius is one unit long). In this special case sin(A) = y/r = y/1 = y and cos(A) = x/r = x/1 = x. This means that for the unit circle the x and y coordinates of point P are the cosine and sine of the angle A. This has several uses. First if we know one coordinate we can find the other by using the Pythagorean Theorem and once we have both coordinates we know the sine and cosine of the angle. Secondly if we are given the x and y coordinates of a point on the circumference of the unit circle we automatically know the cosine and sine of the angle (x and y respectively). Let's look at an example in each of the four quadrants (as we go around the circle).
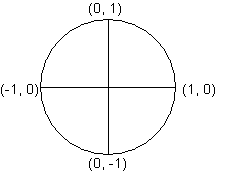 What if our points are along the axes? Let's consider that next. The figure to the right provides information on the coordinates of each point as we go around the unit circle. The calculation of the sine and cosine is shown below:
What if our points are along the axes? Let's consider that next. The figure to the right provides information on the coordinates of each point as we go around the unit circle. The calculation of the sine and cosine is shown below: