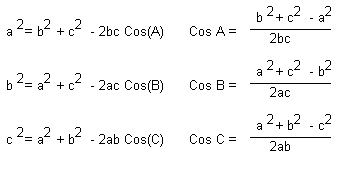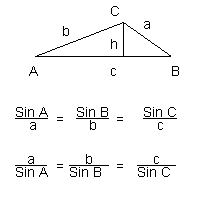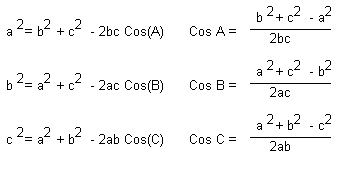Trigonometry Definitions, Identities, Formulas and Equations

Definitions

• csc(q) = 1 / sin(q)
• sec(q) = 1/ cos(q)
• cot(q) = 1 tan(q)
• tan(q) = sin(q) / cos(q)
• cot(q) = cos(q) / sin(q)

Pythagorean Identities

• sin²(q) + cos²(q) = 1
• tan²(q) + 1 = sec²(q)
• cot²(q) + 1 = csc²(q)

Opposite-Angle Formulas

• sin(-q) = - sin(q)
• cos(-q) = cos(q)
• tan(-q) = - tan(q)

Reduction Formulas

• sin(q + 2 π k) = sin(q)
• cos(q + 2 2 π k) = cos(q)
• sin(π / 2 - q) = cos(q)
• cos(π / 2 - q) = sin(q)

Addition Formulas

• sin(s + t) = sin(s) * cos(t) + cos(s) * sin(t)
• sin(s - t) = sin(s) * cos(t) - cos(s) * sin(t)
• cos(s + t) = cos(s) * cos(t) - sin(s) * sin(t)
• cos(s - t) = cos(s) * cos(t) + sin(s) * sin(t)
• tan(s + t) = [ tan(s) + tan(t) ] / [1 - tan(s) * tan(t) ]
• tan(s - t) = [ tan(s) - tan(t) ] / [1 + tan(s) * tan(t) ]

Double-Angle Formulas

• sin(2q) = 2*sin(q)*cos(q)
• cos(2q) = cos²(q) - sin(²(q)
• tan(2q) = [2*tan(q) ] / [ 1 - tan²(q) ]

Half-Angle Formulas

• sin(q)/2) = ± √ [1 - cos(q) ] / 2
  
  
• cos(q)/2) = ± √ [1 + cos(q) ] / 2
  
  
• tan(q)/2) = sin(q) / [ 1 + cos(q) ]

Product-to-Sum Formulas

• sin(A) sin(B) = ½ [ cos(A - B) - cos(A + B) ]
• sin(A> cos(B) = ½ [ sin(A+ B) + sin(A - B) ]
• cos(A) cos(B) = ½ [cos(A + B) + cos(A - B) ]

Sum-to-Product Formulas

• sin(A) + sin(B) = 2 sin[(A + B) / 2] * cos[ (A - B)/2 ]
• sin(A) - sin(B) = 2 cos[(A + B) / 2] * sin[ (A - B)/2 ]
• cos(A) + cos(B) = 2 cos[(A + B) / 2] * cos[ (A - B)/2 ]
• cos(A) - cos(B) = -2 sin[(A + B) / 2] * sin[ (A - B)/2 ]

Unit Circle Values of the x (cos) and y (sin) Coordinates

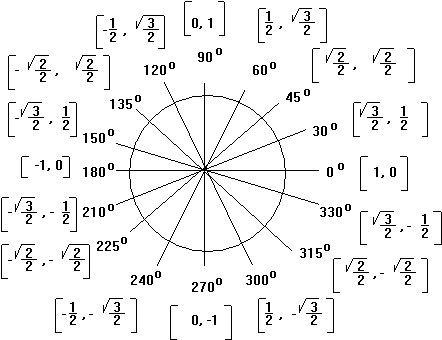
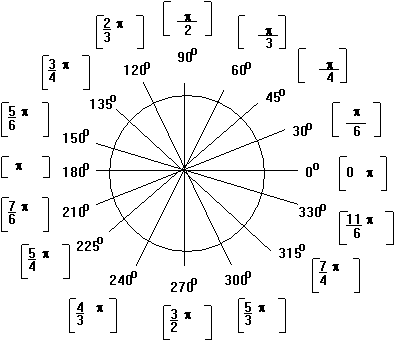
Unit Circle - Degrees and Radians

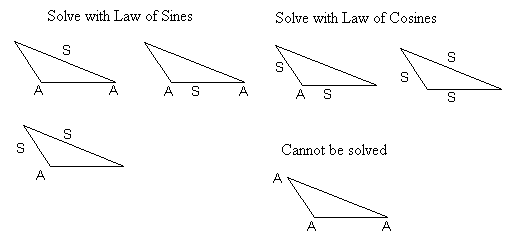
Choosing between Law of Sines and Law of Cosines

Law of Sines

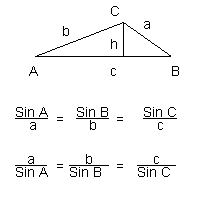
Law of Cosines