Vectors
In this section we will look at the basic concept of a vector, learn to manipulate vectors in basic ways and apply them to problems. As a starting point we will consider a vector as a directed line segment. I have elected to start this way because it is likely that most of your mathematics experience to this point has dealt with straight lines and their manipulation. Our directed line segment will go from one point to another and the direction of the line will be important. To be a vector our line must have a magnitude and a direction. Thus 55 mph is a scalar, not a vector (magnitude but no direction) while 55 mph in a northeastern direction is a vector (magnitude - 55 mph and direction - northeast). Some of the things that can be represented as vectors are:
The velocity of an aircraft where we specify speed and direction
The velocity of a boat, where we specify speed and direction
Forces acting on an object, where we specify magnitude of the force and direction of its action
Changes in populations, where we have a magnitude (number of people) and a directon (increase)
Defining a Vector
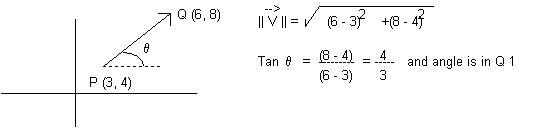 Let's start with a vector that its origin at the point P (3, 4) and its endpoint at Q (6, 8). We will call the vector PQ Where P is the starting point and Q is the end point. The calculation of the magnitude of the vector is shown in the figure to the right. The direction of the vector is given by the tangent and our knowledge of the quadrant the angle of the vector would put it in if the vector started at the origin. This vector would be in the first quadrant so its angle will be between 0o and 90o.
Let's start with a vector that its origin at the point P (3, 4) and its endpoint at Q (6, 8). We will call the vector PQ Where P is the starting point and Q is the end point. The calculation of the magnitude of the vector is shown in the figure to the right. The direction of the vector is given by the tangent and our knowledge of the quadrant the angle of the vector would put it in if the vector started at the origin. This vector would be in the first quadrant so its angle will be between 0o and 90o.
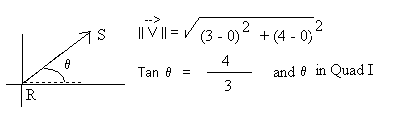 Assume we have a new vector. This vector has its origin at point R (0, 0) and its endpoint at S (3, 4). Calculate the magnitude and direction of this vector and draw a picture of it on a piece of graph paper. Draw a scale on your paper and then draw the vector. Hopefully it will look something like the figure on the right. The vector that you have created is a vector in its own right but it is also an equivalent vector to our original vector PQ. By equivalent we mean that the new vector has the same direction and magnitude as the original vector (magnitude 5 and angle is tan-1(4/3) = . They do not have to start and end at the same points they just have to have the same magnitude and direction (the new vector will be parallel to the old vector).
Assume we have a new vector. This vector has its origin at point R (0, 0) and its endpoint at S (3, 4). Calculate the magnitude and direction of this vector and draw a picture of it on a piece of graph paper. Draw a scale on your paper and then draw the vector. Hopefully it will look something like the figure on the right. The vector that you have created is a vector in its own right but it is also an equivalent vector to our original vector PQ. By equivalent we mean that the new vector has the same direction and magnitude as the original vector (magnitude 5 and angle is tan-1(4/3) = . They do not have to start and end at the same points they just have to have the same magnitude and direction (the new vector will be parallel to the old vector).
Equivalence is an important property, it means that we can move vectors by creating an equivalent vector and placing it in a standard position. For vectors in standard position the initial point is at the origin and the terminal point can be in any quadrant. Next we will address the question of how to build an equivalent vector. To get an equivalent vector we want a new vector that has the same x and y lengths as the old vector. So we find the x length and the y length of the old vector by the following method: xlength = (x terminal - x initial) and ylength = (y terminal - y initial). We can use this information to write the new vector in what is called component form , in this case <3, 4>, 3 units long in the x direction and 4 units long in the y direction. The vector in component form also gives us an equivalent vector with its initial point at the origin. This equivalent vector will go from (0, 0) to (3, 4). To help you practive this take a new vector as specified below, find its magnitude and direction. Write the equivalent vector in component form . Finally determine the initial point and end point for the equivalent vector in standard position.
Practice Problem 1
- Initial point at (-3, -5), Terminal point at (5, 1)
- Determine the magnitude and direction of the vector and an equivalent vector with its Initial point at the origin.
- Solution is at the end of this page
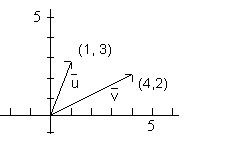 Vector Operations - Now let's talk a little about vector operations such as addition, subtraction and multiplication by a scalar. Get yourself a piece of graph paper, draw an x and y axes and put a scale on the paper that goes from -10 to +10 in both the x and y directions. Now draw the following vectors, u = <1, 3> and v = <4, 2>. Your figure should look something like the figure on the right. The basic vectors are shown with their initial points at the origin. We got the first vector by going 1 unit in the x direction and then 3 units in the y direction. We got the second vector by going 4 units in the x direction and 2 units in the y direction. Now let's consider adding the vectors,
Vector Operations - Now let's talk a little about vector operations such as addition, subtraction and multiplication by a scalar. Get yourself a piece of graph paper, draw an x and y axes and put a scale on the paper that goes from -10 to +10 in both the x and y directions. Now draw the following vectors, u = <1, 3> and v = <4, 2>. Your figure should look something like the figure on the right. The basic vectors are shown with their initial points at the origin. We got the first vector by going 1 unit in the x direction and then 3 units in the y direction. We got the second vector by going 4 units in the x direction and 2 units in the y direction. Now let's consider adding the vectors,
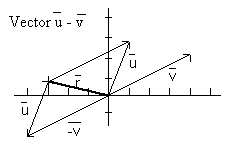
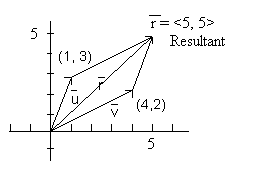 Addition of vectors - u + v. To perform this addition we will place the initial point of one vector on the head of the other vector. It does not matter which vector we start with the answer will be the same, the vector combination will form a parallelogram with parallel sides equal. If we add v to u we follow the upper path in the figure first going along u and then along a vector that is equivalent to v. If we go the other direction and add u to v we follow the lower route in the figure but still end up at the same point. The result of adding the two vectors is called the resultant and is indicated by the vectorr that goes from the origin to the end point (5, 5). In component form the resultant is written as <5, 5>, 5 units in the x direction and then 5 units in the y direction.
Addition of vectors - u + v. To perform this addition we will place the initial point of one vector on the head of the other vector. It does not matter which vector we start with the answer will be the same, the vector combination will form a parallelogram with parallel sides equal. If we add v to u we follow the upper path in the figure first going along u and then along a vector that is equivalent to v. If we go the other direction and add u to v we follow the lower route in the figure but still end up at the same point. The result of adding the two vectors is called the resultant and is indicated by the vectorr that goes from the origin to the end point (5, 5). In component form the resultant is written as <5, 5>, 5 units in the x direction and then 5 units in the y direction.
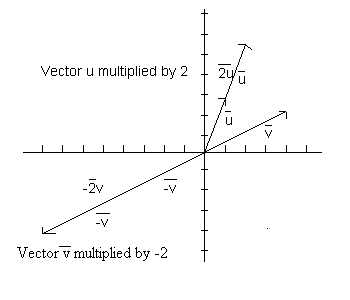 Multiplication of a vector by a scalar - If you multiply a vector by a scalar you change the magnitude of the vector by the scalar factor. If the scalar is greater than 1 you are increasing the magnitude of the vector. If the scalar is between 0 and 1 you are decreasing the magnitude of the vector. If the scalar is negative you are increasing or decreasing the magnitude of the vector and reversing its direction. The figure of the right displays these ideas. If we were doing the addition analytically it would look like this:
Multiplication of a vector by a scalar - If you multiply a vector by a scalar you change the magnitude of the vector by the scalar factor. If the scalar is greater than 1 you are increasing the magnitude of the vector. If the scalar is between 0 and 1 you are decreasing the magnitude of the vector. If the scalar is negative you are increasing or decreasing the magnitude of the vector and reversing its direction. The figure of the right displays these ideas. If we were doing the addition analytically it would look like this:
- u + v = <1, 3> + <4, 2> = <(1 + 4), (3 + 2)> = <5, 5>. We added x coordinate to x coordinate and y coordinate to y coordiate, we added like terms.
- Two times a vector would be 2u = 2<1, 3> = <2*1, 2*3> = <2,6>
- Minus two times a vector would be -2v = -2<4, 2> = <-2*4, -2*2> = <-8, -4>.
- If we were calculating u -v we would have <1, 3> - <4, 2> = <(1 - 4), (3 - 2)> = <-3, -1>.
A Summary of Vector Properties
- u + v = v + u
- (u + v) + w = u + (v + w)
- u + 0 = u
- u - u = 0
- c(du) = (cd)u
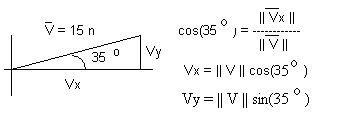 Revisiting the Component Form of a Vector - Assume you are given a vector that has a magnitude of 15 newtons (force) acting at an angle of 35 degrees with the local horizontal. How do we go about putting that vector in component form? The answer is we can use a technique that we have been using all term long. We have a right triangle. The vector is the hypotenuse and the x and y components are the sides of the triangle. If we take the sin and cos of the angle (35o in this case) and then solve for the x and y components of the vector we get the results shown in the figure,
Revisiting the Component Form of a Vector - Assume you are given a vector that has a magnitude of 15 newtons (force) acting at an angle of 35 degrees with the local horizontal. How do we go about putting that vector in component form? The answer is we can use a technique that we have been using all term long. We have a right triangle. The vector is the hypotenuse and the x and y components are the sides of the triangle. If we take the sin and cos of the angle (35o in this case) and then solve for the x and y components of the vector we get the results shown in the figure,
- ux= ||u|| cos(35o).
- uy= ||u|| sin(35o).
This also allows us to write the vector in component form as < ||u|| cos(35o, ||u|| sin(35o>. This says the x component is the magnitude of the vector times the cosine of the angle and y component of the vector is the magnitude of the vector times the sine of the angle. Since the magnitude of the vector is a factor of both components and it is constant we can factor it out and write the vector as ||u||'<'cos(35o), sin(35o)>.
The Concept of the Unit Vector - You were probably hoping that we were done introducing vector concepts but we have one more idea and one more set of notation to cover. The concept is the unit vector. A unit vector is a vector that has a magnitude of 1. A unit vector that points in the same direction as the original vector is a vector with a magnitude of 1 but a direction identical to the original vector. How do we create a unit vector? To create a unit vector pointing in the same direction as the original vector we divide the original vector by its magnitude. For example if we have the vector <-2, 5> its magnitude is Square root[ (-2)2 + (5)2] = Square root(29). The unit vector we want will be <-2/Sqrt(29), 5/Sqrt(29)>. If you calculate the magnitude of this vector you get 4/29 + 25/29 = 29/29 =1, unit magnitude. If you calculate the sin, cos and tan of this vector you will find that they are identical to the values of those functions for the original vector. We have created a vector that has a magnitude of one and points in the same direction as the original vector. Why have we done this?
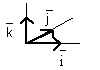 Unit Vectors Along the Major Axes - Believe it or not there was a reason we wanted to be able to create unit vectors. We are now going to use the unit vector concept to define two unit vectors, one along the x axis and one along the y axis. We will call the x axis unit vector ||i|| and the y axis unit vector ||j||. If we were dealing with three dimensions we would also define a ||k|| unit vector that is aligned with the z axis (figure on the right). Restricting ourselves to two dimentsions we can express these unit vectors the following way:
Unit Vectors Along the Major Axes - Believe it or not there was a reason we wanted to be able to create unit vectors. We are now going to use the unit vector concept to define two unit vectors, one along the x axis and one along the y axis. We will call the x axis unit vector ||i|| and the y axis unit vector ||j||. If we were dealing with three dimensions we would also define a ||k|| unit vector that is aligned with the z axis (figure on the right). Restricting ourselves to two dimentsions we can express these unit vectors the following way:
- ||i|| = < 1, 0 >
- ||j|| = < 0, 1 >
If we have a vector specified as <16, 2> we can write it in terms of unit vectors and scalars. <16, 2> = 16<1, 0> + 2<0, 1>
Multiplying will give us <16, 0> + <0, 2> = <16, 2> which is our original vector. To make this even more compact we can write the vector as 16i + 2j. This says we can write any vector in terms of constants times unit vectors. If we want to perform addition we add i components to i components and j components to j components. For example to add 3i + 6j and 6 i + 2 j we would add the like components and get (3 + 6)i + (6 + 2)j = 9i +8j.
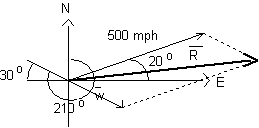 Using Vectors to Solve Problems - Problem 1
Using Vectors to Solve Problems - Problem 1
Problem 1 - Consider the case of an aircraft flying at 500 mph at a heading that is 20o North of East (see figure on the right). Now let's add a wind blowing from 210o at 60 mph. What we would like to do is use vectors to find the actual airspeed of the aircraft and the heading of the aircraft (angle). We will attack this problem two different ways. Both approaches will give the same answer. The first approach will be to use the Law of Cosines and then the Law of Sines to determine airspeed and heading. The second approach will be to use vector components to solve the problem. Both approaches work for this problem. However, for more complex problems the vector component approach is more flexible and is much easier to extent to a problem where there are more than two factors.
The Law of Cosines Approach - As was discussed earlier in this section if we are adding vectors we place the tail of one vector at the head of the other vector thus forming a parallelogram. That has been done in the figure on the right. Angles in a parallelogram add to a total of 360o. In addition opposite angles are equal. We know from the given information that one angle of the parallelogram is 50o. If there are two of these angles there is 360o - 100o = 260o left for the other two angles (which must be equal). So the two big angles in the parallelogram are each 130o. To find the magnitude of the resultant vector we can use the Law of Cosines to write. ||r||2 = 5002 + 602 - 2 (500)(60)cos(130o). The resultant velocity of the aircraft has a magnitude of ||r|| = 540.5 mph. To determine direction we first use the Law of Sines to find the angle between the resultant and the original aircraft vector. sin(angle)/60 = sin(130o/ 540.5. Solving for sin(angle) gives sin(angle) = 0.0850. Using the inverse sine we get sin-1(0.0850) = 4.88o. But the angle we want is 20o - 4.88o = 15.12o North of East (the heading of the aircraft).
The Vector Component Approach - In this case we will find the x and y components of each vector and add them to get the x and y components of the resultant vector. Then we will determine the magnitude and direction of the aircraft using the values for the components.
| x Component | y Component |
|---|
| 500*cos(20o) | 500*sin(20o) |
| 60*cos(30o) | 60*sin(30o) |
| ---------------- | ------------------ |
| 521.81 | 141.01 |
The value of the resultant is the square root of the sum of the components square, 540 mph. The heading angle of the aircraft can be determined as tan-1(141.01/521.81) = 15.12o North or East. These solutions are almost exactly the same as those we found using the Law of Cosines (slight differences due to rounding). We can write our results in vector notation in at least three ways:
- 521.81i + 141.01j
- <521.81, 141.01>
- 540 < cos(15.12o, sin(15.12o) >
Note that all of these are equivalent, they all represent the same thing.
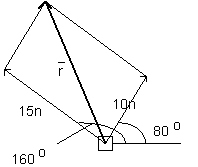 Problem 2 - Let's vary the problem now by looking at the case of two forces acting on a body. One is a 15 newton force acting at an angle of 160o and the other is a 10 newton force acting at an angle of 80o. We want to determine the magnitude and direction of the resultant force. As we did in problem 1 we will first solve this problem using the Law of Cosines and then solve it again using a vector component approach..
Problem 2 - Let's vary the problem now by looking at the case of two forces acting on a body. One is a 15 newton force acting at an angle of 160o and the other is a 10 newton force acting at an angle of 80o. We want to determine the magnitude and direction of the resultant force. As we did in problem 1 we will first solve this problem using the Law of Cosines and then solve it again using a vector component approach..
The Law of Cosines Approach In the figure you see the parallelogram formed when we add the forces. The corner angles already identified in the parallelogram are each160o - 80o = 80o for a total of 160o. That leaves 360o - 160o = 200o for the other two angles, so each of the smaller angles will be 100o. Using the Law of Cosines we have ||r||2 = 102 + 152 - 2 (10)(15)cos(100o). The resultant force on the object has a magnitude of ||r|| = 19.42 newtons. To determine direction we first use the Law of Sines to find the angle between the resultant and the 10 newton force. sin(angle)/15 = sin(100o/ 19.42. Solving for sin(angle) gives sin(angle) = 0.7607. Using the inverse sine we get sin-1(0.7607) = 49.5o. But the angle we want is 80o + 49.5o = 129.5o.
The Vector Component Approach - In this case we will find the x and y components of each vector and add them to get the x and y components of the resultant vector. Then we will determine the magnitude and direction of the resultant force using the values for the components.
| x Component | y Component |
|---|
| 10*cos(80o) | 10*sin(80o) |
| 15*cos(160o) | 15*sin(160o) |
| ---------------- | ------------------ |
| -12.36 | 14.98 |
The value of the resultant is the square root of the sum of the components square, 519.42 newtons. The angle of the force can be determined as tan-1(14.98/12.36) = 50.47o. This is a reference angle. To find the angle of the resultant force we calculate 180o - 50.47o = 129.5o. These solutions are exactly the same as those we found using the Law of Cosines. We can write our results in vector notation in at least three ways:
- -12.36i + 14.98j
- <-12.36, 14.98>
- 19.42 < cos(129.5o, sin(129.5o) >
Note that all of these are equivalent, they all represent the same thing.
Solutions to practice problems
Practice Problem 1
- Given vector: Initial point (-3, -5), Terminal Point (5, 1)
- Magnitude = Square Root [ (5 - (-3))2 + (1-(-5))2] = Square Root(64 + 36) = 10
- Tan-1(6/8) = xxx degrees.
- x component (5 - (-3)) = 8, y component (1 - (-5)) = 6, vector in component form <8, 6>
- Equivalent vector: Initial point (0, 0), Terminal point (8, 6)
- We got the (8, 6) from the fact that the given vector was 8 units long along the x axis and 6 units long along the y axis.
- Magnitude = Square Root [ (8- 0)2 + (6- 0)2] = 10
- Tan-1(6/8) = xxx degrees.
- So, the new vector has the same magnitude and direction as the original vector.
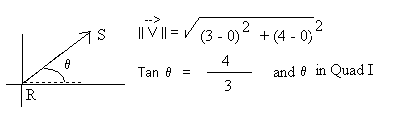 Assume we have a new vector. This vector has its origin at point R (0, 0) and its endpoint at S (3, 4). Calculate the magnitude and direction of this vector and draw a picture of it on a piece of graph paper. Draw a scale on your paper and then draw the vector. Hopefully it will look something like the figure on the right. The vector that you have created is a vector in its own right but it is also an equivalent vector to our original vector PQ. By equivalent we mean that the new vector has the same direction and magnitude as the original vector (magnitude 5 and angle is tan-1(4/3) = . They do not have to start and end at the same points they just have to have the same magnitude and direction (the new vector will be parallel to the old vector).
Assume we have a new vector. This vector has its origin at point R (0, 0) and its endpoint at S (3, 4). Calculate the magnitude and direction of this vector and draw a picture of it on a piece of graph paper. Draw a scale on your paper and then draw the vector. Hopefully it will look something like the figure on the right. The vector that you have created is a vector in its own right but it is also an equivalent vector to our original vector PQ. By equivalent we mean that the new vector has the same direction and magnitude as the original vector (magnitude 5 and angle is tan-1(4/3) = . They do not have to start and end at the same points they just have to have the same magnitude and direction (the new vector will be parallel to the old vector).
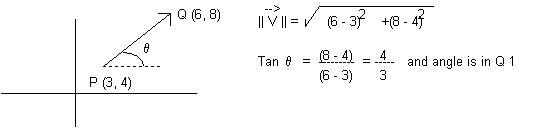 Let's start with a vector that its origin at the point P (3, 4) and its endpoint at Q (6, 8). We will call the vector
Let's start with a vector that its origin at the point P (3, 4) and its endpoint at Q (6, 8). We will call the vector 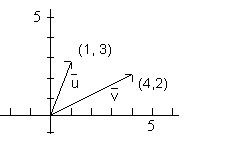 Vector Operations - Now let's talk a little about vector operations such as addition, subtraction and multiplication by a scalar. Get yourself a piece of graph paper, draw an x and y axes and put a scale on the paper that goes from -10 to +10 in both the x and y directions. Now draw the following vectors,
Vector Operations - Now let's talk a little about vector operations such as addition, subtraction and multiplication by a scalar. Get yourself a piece of graph paper, draw an x and y axes and put a scale on the paper that goes from -10 to +10 in both the x and y directions. Now draw the following vectors, 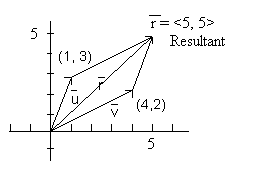 Addition of vectors -
Addition of vectors - 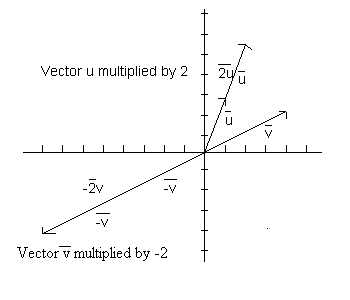 Multiplication of a vector by a scalar - If you multiply a vector by a scalar you change the magnitude of the vector by the scalar factor. If the scalar is greater than 1 you are increasing the magnitude of the vector. If the scalar is between 0 and 1 you are decreasing the magnitude of the vector. If the scalar is negative you are increasing or decreasing the magnitude of the vector and reversing its direction. The figure of the right displays these ideas. If we were doing the addition analytically it would look like this:
Multiplication of a vector by a scalar - If you multiply a vector by a scalar you change the magnitude of the vector by the scalar factor. If the scalar is greater than 1 you are increasing the magnitude of the vector. If the scalar is between 0 and 1 you are decreasing the magnitude of the vector. If the scalar is negative you are increasing or decreasing the magnitude of the vector and reversing its direction. The figure of the right displays these ideas. If we were doing the addition analytically it would look like this:

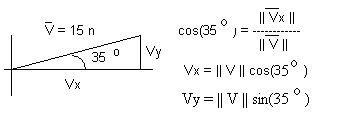 Revisiting the Component Form of a Vector - Assume you are given a vector that has a magnitude of 15 newtons (force) acting at an angle of 35 degrees with the local horizontal. How do we go about putting that vector in component form? The answer is we can use a technique that we have been using all term long. We have a right triangle. The vector is the hypotenuse and the x and y components are the sides of the triangle. If we take the sin and cos of the angle (35o in this case) and then solve for the x and y components of the vector we get the results shown in the figure,
Revisiting the Component Form of a Vector - Assume you are given a vector that has a magnitude of 15 newtons (force) acting at an angle of 35 degrees with the local horizontal. How do we go about putting that vector in component form? The answer is we can use a technique that we have been using all term long. We have a right triangle. The vector is the hypotenuse and the x and y components are the sides of the triangle. If we take the sin and cos of the angle (35o in this case) and then solve for the x and y components of the vector we get the results shown in the figure,
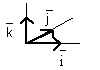 Unit Vectors Along the Major Axes - Believe it or not there was a reason we wanted to be able to create unit vectors. We are now going to use the unit vector concept to define two unit vectors, one along the x axis and one along the y axis. We will call the x axis unit vector ||
Unit Vectors Along the Major Axes - Believe it or not there was a reason we wanted to be able to create unit vectors. We are now going to use the unit vector concept to define two unit vectors, one along the x axis and one along the y axis. We will call the x axis unit vector || Using Vectors to Solve Problems - Problem 1
Using Vectors to Solve Problems - Problem 1
 Problem 2 - Let's vary the problem now by looking at the case of two forces acting on a body. One is a 15 newton force acting at an angle of 160o and the other is a 10 newton force acting at an angle of 80o. We want to determine the magnitude and direction of the resultant force. As we did in problem 1 we will first solve this problem using the Law of Cosines and then solve it again using a vector component approach..
Problem 2 - Let's vary the problem now by looking at the case of two forces acting on a body. One is a 15 newton force acting at an angle of 160o and the other is a 10 newton force acting at an angle of 80o. We want to determine the magnitude and direction of the resultant force. As we did in problem 1 we will first solve this problem using the Law of Cosines and then solve it again using a vector component approach..