Relations and Functions and Their Domains and Ranges
When you have finished this lesson you should be able to:
- fully explain and interpret functional notation
- evaluate a function using a formula
- determine input values when given output values and output values when given input values
- determine input and output values from tables and graphs
- find the inverse of a function
- determine the domain and range of a function
Relations and Functions
The most general type of link between two quantities is called a relation. In a relation each x value (domain value) maps to one or more y value (range value)
Example: 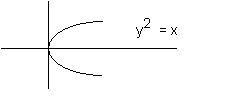 y2 = x, In this case there are two values of y for every value of x since y is equal to plus or minus the square root of x. The requirement for a relation is that there be one or more values of y for every value of x. That requirement is fulfilled by the example.
y2 = x, In this case there are two values of y for every value of x since y is equal to plus or minus the square root of x. The requirement for a relation is that there be one or more values of y for every value of x. That requirement is fulfilled by the example.
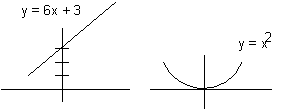 In a function, as opposed to a relation each x value (domain value) maps to exactly one, and only one range value (y value). Note that all of the x values may map to the same value of y. The requirement is that each x maps to one y value. There is no requiement that each x map to a different value of y. y = 6x + 3 and y = x2 are examples of functions, each x maps to one and only one value of y.
In a function, as opposed to a relation each x value (domain value) maps to exactly one, and only one range value (y value). Note that all of the x values may map to the same value of y. The requirement is that each x maps to one y value. There is no requiement that each x map to a different value of y. y = 6x + 3 and y = x2 are examples of functions, each x maps to one and only one value of y.
Next we are going to take a deeper look at functions and the notation that goes with them.
Functional Notation - Input and Output - An example of functional notation is d = g(t) = 16(t)2. In this case we are saying that d (distance traveled) is a function of t, here g(t) and the particular function is 16(t)2. If we want to evaluate distance traveled at a particular time, say 2 seconds, we could write d = g(t=2) = 16(2)2. That is the way we could write it, but we don't write it that way (we use a notational form that was first used by Leonhard Euler around 1734). The notation that is used expresses the idea by writting it as g(2) = 16(2)2. In other words the argument of g( ? ) is the value of t that we want to use and everywhere in the function we replace t with that value. So if we had h(x) = 2x2 + 6x and we wanted to determine the value of the function when x was equal to -4 we would write it as h(-4) = 2(-4)2 + 6(-4) = 2(16) - 24 = 32 - 24 = 8.
To illustrate the idea consider the following examples:
- m(t) = 2(t)3 - 6t2, when t = -1 we have m(-1)=2(-1)3 - 6(-1)2=-2 + 6 = 4
- w(s)= 2s2 - 4s, when s = a we have w(a) = 2(a)2 - 4(a) = 2a2 - 4a
- m(x) = 1/x + 3x, when x = 2x we have m(2x) = 1/(2x) + 3(2x) = 1/2x + 6x
- r(x) = 2x2 - 7x, when x = a- 2 we have
- r(a-2) = 2(a-2)2 - 7(a-2)
- r(a-2 )= 2(a2-4a +4) -7a + 14
- r(a-2)= 2a2-8a + 8- 7a+ 14
- r(a-2)= 2a2 -15a + 22.
Input and Output - When we write a function as, f(x) the x represents the input, when we have a formula and replace all the x's with the value of x the resulting output is the value of the function for that value of x. Let's look at input and output for three cases, (i) we have a formula, (ii) the information is in a table and (iii) the function is represented by a graph.
- We have a formula
Define a function such as: f(x) = 3x2 + 5x - 7
- Select an input value for x, in this case x = -4
- Rewrite the function as: f(-4) = 3(-4)2 + 5(-4) - 7
- Carry out the arithmetic to get: f(-4) = 3(16) - 20 - 7 = 48-27 = 21
- When x = -4 (input) the value of the function is 21 (output)
- The information is contained in a table such as the one shown below. The table is designed to provide data on the age of a human fetus (weeks since conception) as a function of the size of a body part (the foot) measured in mm. The function can be written as A(l) (age is a function of length). If we wanted the value of f(20 mm) we would look for 20 mm in the foot length row and then look for the corresponding value of age, 14 weeks. Conversely, we could be given A(?) = 30, meaning the age is predicted to be 30 weeks but we want the length of a foot (in mm). In this case we would go to the age row to find 30 and then look for the corresponding value of foot length, 63 mm.
| Foot length (mm) | 9 | 20 | 39 | 50 | 63 | 83 |
| Age (weeks) | 10 | 14 | 20 | 24 | 30 | 38 |
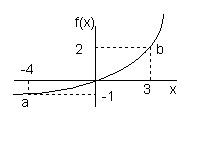 The function is described by a graph.
The function is described by a graph.
In the figure on the right two points have been selected (-4, -1) and (3, 2). We will use the first point to illustrate the treatment of input. f(-4) means the value of the function when x = -4. We go along the x axis to minus 4 and then drop a vertical line to the curve. Next we draw a horizontal line from the curve to the y axis. It intersects the axis at -1 so the value of the function when x = -4 [ f(-4) ] is -1 or f(-4) = -1. Now using the right most point if we are told that f(x) = 2 we go up the y axis (f(x) axis) until we come to 2, then horizontally until we hit the graph and finally vertically until we hit the x axis at x = 3. This says that when f(x) = 2 the value of x is 3. [Remember there could be more than one value of x that gives us this value of f(x)].
Range and Domain of a Function
Domain of a function: The domain of a function consists of all of the values of the independent variable (usually X ) for which the function is defined.
For example
- f(x) = 1/x is defined for all values of x except x = 0 (you cannot divide by zero)
- f(x) = x2 is defined for all values of x.
Range of a function:The range of a function consists of all of the values of the function as the independent variable (x) varies over its domain.
Using the previous examples
- the range of f(x) = 1/x is from -infinity up to zero and from zero to plus infinity (does not include zero)
- the range of f(x) = x2 is from zero to plus infinity (the function is never negative)
Zeroes of a function:
Inputs to the function (x values) that make the value of the function equal to zero.
Examples:
- f(x) = 9x, When x = 0, f( 0 ) = 9*0 = 0, so x = 0 is a zero of the function
- f(x) = 4x - 2, When x = 1/2 , f( 1/2 ) = 4*(1/2) - 2 = 0, so x = 1/2 is a zero of the function.
- f(x) = x2 -2x - 3 Factor to get (x - 3) (x + 1)
- Equate (x - 3) and (x + 1) to zero. This yields x = 3 and x = -1
- When x = 3, f(3) = 32 - 2*3 - 3 = 0 , so x = 3 is a zero of the function
- When x = -1, f(-1) = (-1)2 -2*(-1) - 3 = 0, so x = 1 is also a zero of the function.
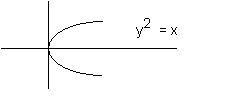 y2 = x, In this case there are two values of y for every value of x since y is equal to plus or minus the square root of x. The requirement for a relation is that there be one or more values of y for every value of x. That requirement is fulfilled by the example.
y2 = x, In this case there are two values of y for every value of x since y is equal to plus or minus the square root of x. The requirement for a relation is that there be one or more values of y for every value of x. That requirement is fulfilled by the example.
 In a function, as opposed to a relation each x value (domain value) maps to exactly one, and only one range value (y value). Note that all of the x values may map to the same value of y. The requirement is that each x maps to one y value. There is no requiement that each x map to a different value of y. y = 6x + 3 and y = x2 are examples of functions, each x maps to one and only one value of y.
In a function, as opposed to a relation each x value (domain value) maps to exactly one, and only one range value (y value). Note that all of the x values may map to the same value of y. The requirement is that each x maps to one y value. There is no requiement that each x map to a different value of y. y = 6x + 3 and y = x2 are examples of functions, each x maps to one and only one value of y.
 The function is described by a graph.
The function is described by a graph.