In this section we will deal with the subjects of double angle and half-angle formulas as well as some additional trigonometric identities.
Double Angle Formulas
 The double angle formulas are written in the form sin(2*angle), cos(2*angle) and tan(2*angle). They can be used to simplify equations or applied directly to some classes of problems. We will derrive the formula for sin(2*angle). For cos(2*angle) and tan(2*angle) we will merely state the results. The figure on the right shows two right triangles which are reflections of one another. Both have a hypotenuse of length 1. The Horizontal leg of both triangles is equal to cos(theta). This comes from cos(theta) = adjacent side/hypotenuse. Solving for adjacent side we get hypotenuse * cos(theta), but the hypotenuse is 1 so the final answer is just cos(theta). The angle between the horizontal axis and the hypotenuse is theta for both triangles so the total angle inside the triangle is theta + theta or 2*theta. Now, using the law of sines we can write:
The double angle formulas are written in the form sin(2*angle), cos(2*angle) and tan(2*angle). They can be used to simplify equations or applied directly to some classes of problems. We will derrive the formula for sin(2*angle). For cos(2*angle) and tan(2*angle) we will merely state the results. The figure on the right shows two right triangles which are reflections of one another. Both have a hypotenuse of length 1. The Horizontal leg of both triangles is equal to cos(theta). This comes from cos(theta) = adjacent side/hypotenuse. Solving for adjacent side we get hypotenuse * cos(theta), but the hypotenuse is 1 so the final answer is just cos(theta). The angle between the horizontal axis and the hypotenuse is theta for both triangles so the total angle inside the triangle is theta + theta or 2*theta. Now, using the law of sines we can write:
- sin(2*theta)/2*sin(theta) = sin(alpha)/1
- sin(alpha) can also be written as cos(theta)/1 (opposite side over hypotenuse)
- substituting this in our first expression gives sin(2*theat)/2*sin(theta) = cos(theta)
- solving for sin(2*theta) gives sin(2*theta) = 2*sin(theta)*cos(theta)
We now have a formula that says sin(2*theta) = 2*sin(theta)*cos(theta). If is important to note that sin(2*theta) IS NOT EQUAL TO 2*sin(theta). To take an example we will use the formula to calculate the sin of twice 30o. Based on our formula this would be written as:
- sin(2*30o) = 2*sin(30o)*cos(30o)
- = 2*(0.5)*(0.866) = 0.8660
There are double angle formulas shown in the text for sine, cosine and tangent. The formulas are as follows:
- sin(2*theta) = 2*sin(theta)*cos(theta)
- cos(2*theta) = cos2(theta) - sin2(theta)
- Alternative form: cos(2*theta) = 1 - 2*sin2(theta)
- Alternative form: cos(2*theta) = 2*cos2(theta) - 1
- tan(2*theta) = [2*tan(theta)]/[1 - tan2(theta)]
Half Angle Formulas
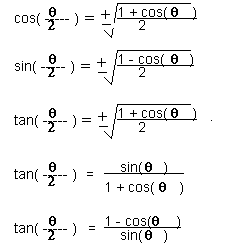 Just as the double angle formulas dealt with the problem of finding the trigonometric function of twice an angle (2*theta) the half-angle formulas deal with the problem of finding the trigonometric function of half of an angle (theta/2). The half-angle formulas we will use are shown on the right. Note that the sine and cosine forumlas and one version of the tngent formula have a + or - sign in front of them. This means that you will first determine whether the result will be positive or negative How will you make this determination?
Just as the double angle formulas dealt with the problem of finding the trigonometric function of twice an angle (2*theta) the half-angle formulas deal with the problem of finding the trigonometric function of half of an angle (theta/2). The half-angle formulas we will use are shown on the right. Note that the sine and cosine forumlas and one version of the tngent formula have a + or - sign in front of them. This means that you will first determine whether the result will be positive or negative How will you make this determination?
Take the original problem and determine the limits on the angle that are given. For example if you are told the angle is in quadrant II you know that the angle must be between 90o and 180o. Dividing through by 2 we know that the half angle (theta/2) must be between 45o and 90o. This makes it a first quadrant angle and the appropriate sign is +. Let's Do some sample problems to get the hang of this determination:
- Beta is a third quadrant angle
- Beta is between 180o and 270o
- Dividing by 2 we know that Beta/2 must be between 90o and 135o (second quadrant)
- If we want the cosine of Beta/2 we use the - sign.
- If we want the sine of Beta/2 we use the + sign.
- If we want the tangent of Beta/2 we use the - sign.
- Angle Alpha is 400o
- Half of angle Alpha is 400/2 = 200o
- 200o is a third quadrant angle
- If we want the cosine of Alpha/2 we use the - sign.
- If we want the sine of Alpha/2 we use the - sign.
- If we want the tangent of Alpha/2 we use the + sign.
 The double angle formulas are written in the form sin(2*angle), cos(2*angle) and tan(2*angle). They can be used to simplify equations or applied directly to some classes of problems. We will derrive the formula for sin(2*angle). For cos(2*angle) and tan(2*angle) we will merely state the results. The figure on the right shows two right triangles which are reflections of one another. Both have a hypotenuse of length 1. The Horizontal leg of both triangles is equal to cos(theta). This comes from cos(theta) = adjacent side/hypotenuse. Solving for adjacent side we get hypotenuse * cos(theta), but the hypotenuse is 1 so the final answer is just cos(theta). The angle between the horizontal axis and the hypotenuse is theta for both triangles so the total angle inside the triangle is theta + theta or 2*theta. Now, using the law of sines we can write:
The double angle formulas are written in the form sin(2*angle), cos(2*angle) and tan(2*angle). They can be used to simplify equations or applied directly to some classes of problems. We will derrive the formula for sin(2*angle). For cos(2*angle) and tan(2*angle) we will merely state the results. The figure on the right shows two right triangles which are reflections of one another. Both have a hypotenuse of length 1. The Horizontal leg of both triangles is equal to cos(theta). This comes from cos(theta) = adjacent side/hypotenuse. Solving for adjacent side we get hypotenuse * cos(theta), but the hypotenuse is 1 so the final answer is just cos(theta). The angle between the horizontal axis and the hypotenuse is theta for both triangles so the total angle inside the triangle is theta + theta or 2*theta. Now, using the law of sines we can write:
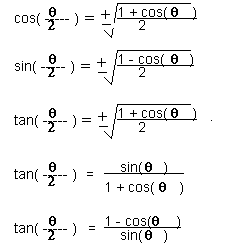 Just as the double angle formulas dealt with the problem of finding the trigonometric function of twice an angle (2*theta) the half-angle formulas deal with the problem of finding the trigonometric function of half of an angle (theta/2). The half-angle formulas we will use are shown on the right. Note that the sine and cosine forumlas and one version of the tngent formula have a + or - sign in front of them. This means that you will first determine whether the result will be positive or negative How will you make this determination?
Just as the double angle formulas dealt with the problem of finding the trigonometric function of twice an angle (2*theta) the half-angle formulas deal with the problem of finding the trigonometric function of half of an angle (theta/2). The half-angle formulas we will use are shown on the right. Note that the sine and cosine forumlas and one version of the tngent formula have a + or - sign in front of them. This means that you will first determine whether the result will be positive or negative How will you make this determination?