Reference Angles
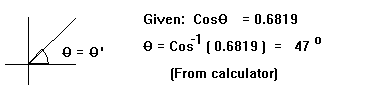 A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
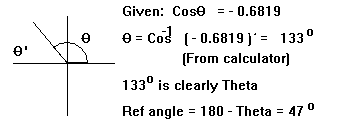 In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
 None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
 In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
-------Signs of the Trigonometric Functions------
| Quadrant | Sine | Cosine | Tangent |
|---|
| 1 | + | + | + |
| 2 | + | - | - |
| 3 | - | - | + |
| 4 | - | + | - |
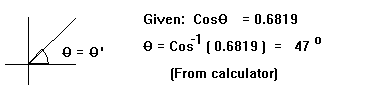 A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
A reference angle is the angle between the terminal side of an angle and the x axis. In the first quadrant the reference angle and the angle are the same. The trigonometric functions of an angle are the same as those of its reference angle with the proper sign (plus or minus) placeed in front based on the quadrant that contains the terminal side of the angle. In the first quadrant all of the signs are positive. So, given that the cosine of our angle is 0.6819 we calculate the inverse cosine and place a positive sign in front of it. The answer, from a calculator is 47 degrees.
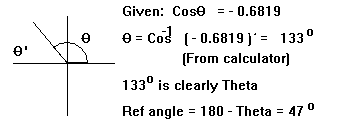 In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
In the second quadrant the cosine is negative. The inverse cosine of -0.6819 gives us the correct angle of 133 degrees. Note that had we been given the sine of the angle the inverse sign would not have given us a second quadrant solution since the inverse sign will only return angles between -90o and +90o. The inverse cosine is defined between 0o and 180o so it gave us a second quadrant solution.
 None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
None of the inverse trigonometric functions will give us a direct solution when we have an angle in the third quadrant. Using the inverse we get an answer of 133o. Clearly, this is not a third quadrant angle. But, if we calculate the reference angle (180 - 133) = 47o and then add the reference angle to 180o we get the correct solution 180o + 47o = 227o.
 In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below:
In the fourth quadrant the inverse cosine gives an answer of 47o. Clearly this is not a fourth quadrant angle. The correct angle is 360o - 47o or 313o. In this case, as in most of the others you need to determine which quadrant you are in and then decide what information the inverse trigonometric function is providing. The signs of the trigonometric functions in the various quadrants are shown in the table given below: